Serret-Frenet formulae
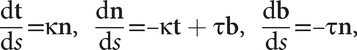
where τ denotes torsion. If the torsion of a curve is 0, then the curve is planar. κ(s) and τ(s) determine a curve up to isometry.
- AMS
- An
- analog device
- analysis
- analysis of variance
- analysis situs
- analytic
- analytic
- analytic continuation
- analytic geometry
- analytic number theory
- analytics
- and
- angle
- angle
- angle
- angle
- angle
- angle of depression/elevation
- angle of friction
- angle of inclination
- angle of projection
- angular acceleration
- angular frequency
- angular measure