“simplex method”的概念、定义、习题解题方法及翻译-数学辞典

(i) introduce slack variables, s and t, to rewrite each inequality as an equation, giving x+2y+s−20 = 0 and 2x+y+t−15 = 0;

(ii) introduce all other slack variables into each equation with a coefficient of zero, giving x+2y+s+0t−20 = 0 and 2x+y+0s+t−15 = 0;

(iii) rewrite the objective function in standard form, including all slack variables with a coefficient of zero, giving P−2x−3y+0s+0t = 0.

The simplex tableau is a table which shows the current values for each variable in each constraint, with the last row, known as the objective row, showing the values in the equation derived from the objective function. The simplex algorithm is the process by which that table is manipulated in order to find the optimal solution. In the solution, the algorithm will produce a series of tableaux.

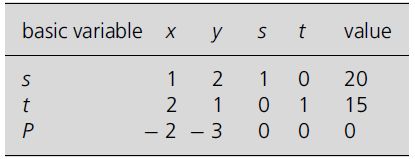
The optimality condition is that when the objective row shows zero in all columns representing basic variables and no negative entries, then it represents an optimal solution.

The standard procedure to achieve this condition is to repeat the following set of steps until all the basic variables, x and y, have been set to zero.

(i) Choose the variable with the largest negative entry in the objective row. The column it is in is called the pivotal column and it is known as the entering variable. In the example y is the entering variable, and the pivotal column is the third from the left.

(ii) For each row of the tableau, divide the value (in the last column) by the entering variable. In the example this gives 20/2 = 10 and 15/1 = 15. The smallest of these determines the pivotal row of the tableau at this stage and the leaving variable, which is s in the example. The pivot is the cell in both the pivotal column and the pivotal row, i.e. 2 in this case.

(iii) Divide all entries in the pivotal row by the pivot, so the row reads s, 0.5, 1, 0.5, 0, 10 in the example.

(iv) Add or subtract multiples of this row to (or from) each other to make the other entries in the pivotal column zero. So it has to be subtracted once from the t row, and added three times to the P row, leaving the tableau looking like this:

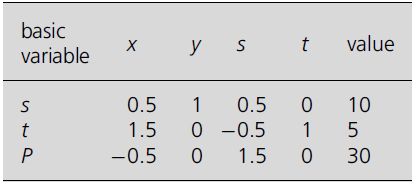
The process would now be repeated, and x will now be the entering variable, and the values at step 2 are 20 for s, and 10/3 for t, so t is the leaving variable, and at step 3 the pivotal row will read t, 1, 0, −1/3, 2/3, 10/3.

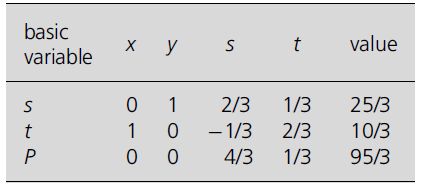
For a many-variable problem this would have to be repeated for each variable in turn, but in this simple example the optimality condition is now satisfied and the maximum value of P is 95/3 occurring when s = 4/3 and t = 1/3, corresponding to x = 10/3 and y = 25/3. In this simple problem, the solution could have been found much more quickly by the vertex method, but the simplex method is an important tool because it can be applied to more complicated problems.