单词

Taylor's Theorem

释义

Taylor's Theorem

Applied to a suitable function f, Taylor's Theorem gives a polynomial that is an approximation to f(x).

Theorem

Let f be a real function on an open interval I, such that the derived functions f(r )(r = 1,…, n) are continuous functions and suppose that a ε I. Then, for all x in I,

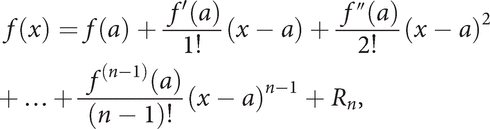
where Rn denotes the remainder term Rn.

Two possible forms for Rn are

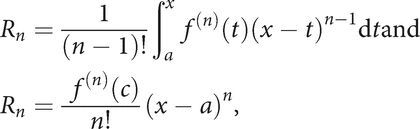
where c lies between a and x. By taking x = a + h, where a + h ε I, the formula

is obtained. This enables f(a + h) to be determined up to a certain degree of accuracy, the remainder Rn giving the error. Suppose now that f is infinitely differentiable in I and that Rn → 0 as n → ∞; then an infinite series can be obtained whose sum is f(x). In such a case, it is customary to write

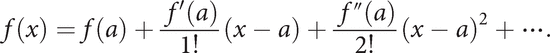
This is the Taylor series (or expansion) for f at (or about) a. The special case with a = 0 is the Maclaurin series for f. Note that the Taylor series of an infinitely differentiable function f(x) can converge without converging to f(x); it is important that the remainder term tends to 0. For example, the function

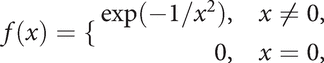
is infinitely differentiable at 0 with f(n)(0) = 0 for all n. Thus, the Taylor series converges, but to the zero function, rather than to f(x).

The Taylor series for a real function f(x,y) of two variables, which has partial derivatives of all orders, states that

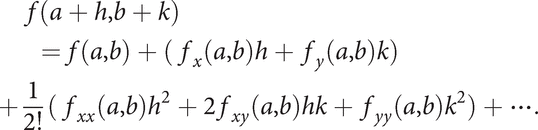
In complex analysis, a function f(z) which is holomorphic at a point a has a Taylor series

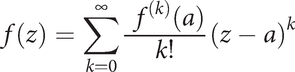
which is convergent in a neighbourhood of a. See also Cauchy's formula for derivatives.

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。