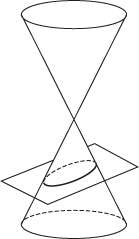
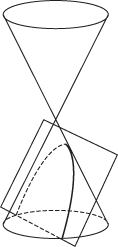
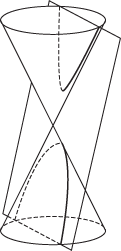
conic
An ellipse
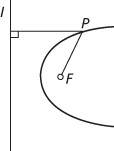
But there are other more convenient characterizations, one of which is by means of the focus and directrix property. Let F be a fixed point (the focus) and l a fixed line (the directrix), not through F, and let e be a fixed positive number (the eccentricity). Then the locus of all points P such that the distance from P to F equals e times the distance from P to l is a curve, called a conic. The conic is called an ellipse if e < 1, a parabola if e = 1 and a hyperbola if e>1. Note that a circle is a conic, but it can only be obtained as a limiting form of an ellipse as e → 0 and the directrix moves to infinity.
A parabola
In a Cartesian coordinate system, a conic has an equation of the form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. For an ellipse, parabola, or hyperbola it is the case that h2– ab is negative, zero, or positive respectively. This general degree two equation can also represent degenerate conics.
The polar equation of a conic is normally obtained by taking the origin at a focus of the conic and the direction given by θ = 0 perpendicular to the directrix. Then the equation can be written l/r = 1 + e cos θ (all θ such that cos θ ≠ −1/e), where e is the eccentricity and l is another constant.
A hyperbola
A parabola

http://www.shodor.org/interactivate/activities/ConicFlyer/
• An interactive demonstration of a conic section.
- great circle
- greatest common divisor
- greatest integer function
- greatest lower bound
- greatest value
- greedy algorithm
- Green, George
- Green's function
- Green's theorem
- Green-Tao theorem
- Gregory, James
- Gregory–Newton forward difference formula
- Grelling's paradox
- Grothendieck, Alexander
- group
- group action
- group algebra
- grouped data
- group table
- Gödel, Kurt
- Gödel numbering
- Gödel's Completeness Theorem
- Gödel's Incompleteness Theorems
- h
- Haar measure