difference equation

Suppose that the terms satisfy the second‐order difference equation un + 2 + aun + 1 + bun = 0. Let α and β be the roots of the quadratic ‘auxiliary equation' x2 + ax + b = 0. If α ≠ β, then un = Aαⁿ + Bβⁿ, and if α = β ≠ 0, then un = (A + Bn)αⁿ, where A and B are arbitrary constants. For example, the Fibonacci sequence is given by the difference equation un + 2 = un + 1 + un, with u0 = 1 and u1 = 1, and the above method gives Binet's formula

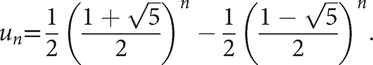
The above theory generalizes to linear constant coefficient difference equations (see linear equation) of higher orders, with the solutions forming a vector space with dimension equalling the order. The solutions to an inhomogeneous linear difference equation are a particular solution added to the homogeneous solutions. Difference equations, also called recurrence relations, do not necessarily have constant coefficients like those considered above. Such difference equations may be approached using generating functions.

• observer
• obtuse angle
• octagon
• octahedron
• octal
• octant
• octonion
• oct‐
• odd function
• odd integer
• odd part
• odd permutation
• odds
• odds ratio
• ODE
• off diagonal
• omega
• one
• one-way function
• one‐sided surface
• one‐sided test
• one‐tailed test
• one‐to‐many
• one‐to‐one
• one‐to‐one correspondence