differential form

where f1,f2,f3 are differentiable real functions of x,y,z. The exterior derivative d maps 0-forms to 1-forms via the chain rule

Note how the terms here are the same as those that appear in the gradient of f. More generally, the exterior derivative takes k-forms to (k + 1)-forms, but the product used is the exterior product, so that, for example, dx dy = –dy dx and dx2 = 0. In the case of applying d to a 1-form we get

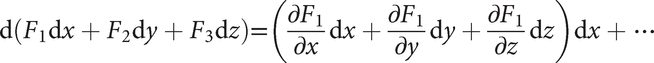
once simplified. Note how the terms here are the same as those that appear in the curl of (F1,F2,F3). A similar calculation shows that d acts like divergence when mapping 2-forms to 3-forms.

In general, d2 = d∘d = 0 generalizing curl(grad) = 0 and div(curl) = 0. Differential forms generalize to Rn for all n and to manifolds where they can be expressed in terms of local coordinates. See Stokes' Theorem (generalized form).

• distribution function
• distribution‐free methods
• distributive
• div
• diverge
• divergence
• divergence theorem
• divides
• divisible
• division
• division
• division algebra
• Division Algorithm
• division ring
• divisor
• divisor function
• divisor of zero
• dodecagon
• dodecahedron
• Dodgson, Charles Lutwidge
• domain
• domain
• domain
• dominated convergence theorem
• Donaldson, Simon