“ellipse”的概念、定义、习题解题方法及翻译-数学辞典

More precisely, we may define an ellipse as a conic with eccentricity less than 1. Thus, it is the locus of all points P such that the distance from P to a fixed point F1 (the focus) equals e (<1) times the distance from P to a fixed line l1 (the directrix). It turns out that there is another point F2 and another line l2 such that the same locus would be obtained with these as focus and directrix. An ellipse is also the conic section that results when a plane cuts a cone in such a way that a bounded section is obtained (see conic).

The line through F1 and F2 is the major axis, and the points V1 and V2 where it cuts the ellipse are the vertices. The length |V1V2| is the length of the major axis and is usually taken to be 2a. The midpoint of V1 V2 is the centre of the ellipse. The line through the centre perpendicular to the major axis is the minor axis, and the distance, usually taken to be 2b, between the points where it cuts the ellipse is the length of the minor axis. The three constants a, b, and e are related by e2 = 1 − b2/a2. The eccentricity e determines the shape of the ellipse. The value e = 0 is permitted and gives rise to a circle, though this requires the directrices to be infinitely far away, invalidating the focus and directrix description.

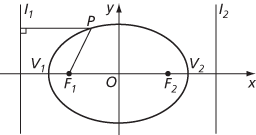
An ellipse in normal form

By taking a coordinate system with origin at the centre of the ellipse and x‐axis along the major axis, the foci have coordinates (ae, 0) and (−ae, 0), the directrices have equations x = a/e and x = −a/e, and the ellipse has equation

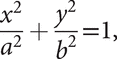
where a > b > 0 (see normal form). This ellipse may be parameterized by x = a cosθ, y = b sinθ (0 ≤ θ < 2π) as parametric equations.

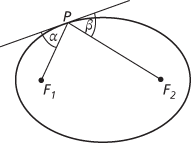
Ellipse highlighting property (ii)

The ellipse has two important properties:

(i) If P is any point of the ellipse with foci F1 and F2 and length of major axis 2a, then |PF1| + |PF2| = 2a. The fact that an ellipse can be seen as the locus of all such points is the basis of a practical method of drawing an ellipse using a string between two points.

(ii) For any point P on the ellipse, let α be the angle between the tangent at P and the line PF1, and β the angle between the tangent at P and the line PF2, as shown in the figure; then α = β. This property is analogous to that of the parabolic reflector (see parabola).