| 释义 |
greatest common divisor (highest common factor) For two non‐zero integers a and b, any integer that is a divisor of both is a common divisor. Of all the common divisors, the greatest is the greatest common divisor (or gcd), denoted by (a,b) or gcd(a,b). The gcd of a and b has the property of being divisible by every other common divisor of a and b. Bézout's lemma states that there are integers s and t such that the gcd can be expressed as sa + tb. If the prime decompositions of a and b are known, the gcd is easily found: for example, if a = 168 = 23 × 3 × 7 and b = 180 = 22 × 32 × 5, then the gcd is 22 × 3 = 12. Otherwise, the gcd can be found by the Euclidean Algorithm, which can also be used to find s and t to express the gcd as sa + tb. Similarly, any finite set of non‐zero integers a1, a2,…, an has a gcd, denoted by (a1, a2,…, an), and there are integers s1, s2,…, sn such that this can be expressed as 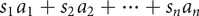 . .
|
 .
.