“Newton's method”的概念、定义、习题解题方法及翻译-数学辞典

单词

Newton's method

释义

Newton's method

The following method of finding successive approximations to a root of an equation f(x) = 0. Suppose that x0 is a first approximation, known to be quite close to a root. If the root is in fact x0 + h, where h is ‘small', taking the first two terms of the Taylor series gives f(x0 + h) ≈ f(x0) + hf′(x0). Since f(x0 + h) = 0, it follows that h ≈ −f(x0)/ f′(x0). Thus x1, given by

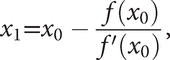
is likely to be a better approximation to the root. To see the geometrical significance of the method, suppose that P0 is the point (x0, f(x0)) on the curve y = f(x), as shown in the first figure. The value x1 is given by the point at which the tangent to the curve at P0 meets the x-axis. It may be possible to repeat the process to obtain successive approximations x0, x1, x2,…, where

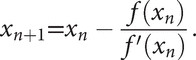
Iterations converge to root

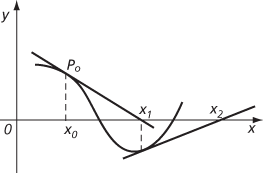
Iterations diverge

These may be successively better approximations to the root as required, but in the second figure is shown the graph of a function, with a value x0 close to a root, for which x1 and x2 do not give successively better approximations. However, if f″(x) is a continuous function and f′(x) is non-zero, then Newton's method quadratically converges to the root in some neighbourhood of the root.

For a system of k equations in k variables, f(x) = 0, the iteration becomes

where J denotes the Jacobian matrix of f.

随便看

数学辞典收录了4151条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。