integral
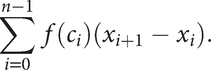
Geometrically, this gives the sum of the areas of n rectangles, and is an approximation to the area under the curve y = f(x) between x = a and x = b.
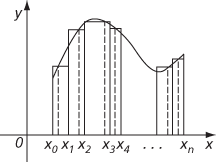
Area represented by a Riemann sum
The (Riemann) integral of f over [a, b] is defined to be the limit I, if it exists, of such a Riemann sum as n, the number of points, increases and the maximal length of the subintervals tends to zero. The value of I is denoted by
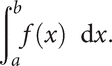
The intention is that the value of the integral is equal to what is intuitively understood to be the signed area under the curve y = f(x). (See Darboux integral.) Such a limit does not always exist, but it can be proved that it does if f is a continuous function on [a,b]. An example where the limit does not exist is the Dirichlet function.
If f is continuous on [a,b] and F is defined by
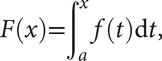
then F′(x) = f(x) for all x in [a, b], so that F is an antiderivative of f. Moreover, if an antiderivative ϕ of f is known, the Fundamental Theorem of Calculus evaluates the integral
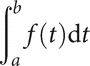
as ϕ(b)−ϕ(a). Of the two integrals
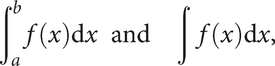
the first, with limits, is called a definite integral; the second, which denotes an antiderivative of f, is an indefinite integral and is defined only up to addition by arbitrary constant. See also Lebesgue measure, line integral, multiple integral, surface integral.
- tension
- tensor
- tensor product
- tera-
- term
- terminal speed
- terminating decimal
- ternary relation
- ternary representation
- tessellation
- test function
- test statistic
- tetra-
- tetrahedral number
- tetrahedron
- TeX
- t-formulae
- Thales of Miletus
- theorem
- Theorema Egregium
- theorem proving
- there exists
- theta function
- Thom, René Frédéric
- Thomson, William