power series

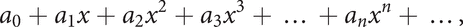
in ascending powers of x, with coefficients a0, a1, a2,…, is a power series in x. For example, the geometric series 1 + x + x2 + … + xⁿ + … is a power series; this has a sum to infinity (see series) only if −1 < x < 1 when considered as a real power series or for |x|<1 when considered as a complex power series.

Real and complex power series converge (that is, have a sum to infinity) within a circle of convergence.

The coefficients ai may more generally be taken from a field or commutative ring R. The formal power series in an indeterminate x with coefficients in R themselves form a ring denoted R[[x]]. These power series may be naturally added and multiplied without reference to convergence.

For further examples of power series, see Appendix 11. See also Taylor series.

• minimum capacity
• minimum connector problem
• minimum cost spanning tree
• Minkowski, Hermann
• Minkowski's inequality
• Minkowski space
• minor arc
• minor axis
• minus
• minus or plus
• minus sign
• minute
• mirror‐image
• Mirzakhani, Maryam
• mixed boundary condition
• mixed derivative
• mixed numbers
• mixed strategy
• mode
• model
• model theory
• modular arithmetic
• modular form
• modular group
• modularity theorem