| 释义 |
Prime Number TheoremThe theorem giving an asymptotic form for the Prime Counting Function  for number of Primes less thansome Integer  . Legendre  (1808) suggested that, for large ,
 | (1) |
 and  (where  is sometimes called Legendre's Constant), a formula which is correct inthe leading term only (Wagon 1991, pp. 28-29). In 1791, Gauß became the first to suggest instead
 | (2) |
 | (3) |
 is the Logarithmic Integral. This function has  as the leading term and has been shown to be abetter estimate than alone. The statement (3) is often known as ``the'' prime number theorem and was provedindependently by Hadamard and Vallée Poussin in 1896. A plot of (lowercurve) and is shown above for  .
For small , it has been checked and always found that  . However, Skewes proved that the first crossing of occurs before  (the Skewes Number). The upper bound for the crossing hassubsequently been reduced to 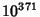 . Littlewood (1914) proved that the Inequality reverses infinitely often forsufficiently large (Ball and Coxeter 1987). Lehman (1966) proved that at least  reversals occur for numberswith 1166 or 1167 Decimal Digits.
Chebyshev (Rubinstein and Sarnak 1994) put limits on the Ratio
 | (4) |
 | (5) |
Hadamard and Vallée Poussin proved the prime number theorem by showing that the Riemann Zeta Function  hasno zeros of the form  (Smith 1994, p. 128). In particular, Vallée Poussin showed that
 | (6) |
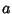 . A simplified proof was found by Selberg and Erdös (1949) (Ball and Coxeter 1987, p. 63).
Riemann estimated the Prime Counting Function with
 | (7) |
 . Riemann (1859) also suggested the Riemann Function
 | (8) |
 is the Möbius Function (Wagon 1991, p. 29). An even better approximation for small (by a factor of 10 for  ) is the Gram Series.
The prime number theorem is equivalent to
 | (9) |
 is the Summatory Mangoldt Function.
The Riemann Hypothesis is equivalent to the assertion that
 | (10) |
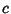 (Ingham 1932, Ball and Coxeter 1987). Some limits obtained without assuming the RiemannHypothesis are
Ramanujan showed that for sufficiently large  ,
 | (13) |
 | (14) |
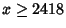 (Berndt 1994, p. 114).See also Bertrand's Postulate, Dirichlet's Theorem, Gram Series, Prime Counting Function,Riemann's Formula, Riemann Function, Riemann-Mangoldt Function,Riemann Weighted Prime-Power Counting Function, Skewes Number
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 62-64, 1987.Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994. Courant, R. and Robbins, H. ``The Prime Number Theorem.'' §1.2c in Supplement to Ch. 1 in What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 27-30, 1996. Davenport, H. ``Prime Number Theorem.'' Ch. 18 in Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, pp. 111-114, 1980. de la Vallée Poussin, C.-J. ``Recherches analytiques la théorie des nombres premiers.'' Ann. Soc. scient. Bruxelles 20, 183-256, 1896. Hadamard, J. ``Sur la distribution des zéros de la fonction  et ses conséquences arithmétiques (').'' Bull. Soc. math. France 24, 199-220, 1896. Hardy, G. H. and Wright, E. M. ``Statement of the Prime Number Theorem.'' §1.8 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 9-10, 1979. Ingham, A. E. The Distribution of Prime Numbers. London: Cambridge University Press, p. 83, 1932. Legendre, A. M. Essai sur la Théorie des Nombres. Paris: Duprat, 1808. Lehman, R. S. ``On the Difference 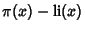 .'' Acta Arith. 11, 397-410, 1966. Littlewood, J. E. ``Sur les distribution des nombres premiers.'' C. R. Acad. Sci. Paris 158, 1869-1872, 1914. Nagell, T. ``The Prime Number Theorem.'' Ch. 8 in Introduction to Number Theory. New York: Wiley, 1951. Riemann, G. F. B. ``Über die Anzahl der Primzahlen unter einer gegebenen Grösse.'' Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671, 1859. Rubinstein, M. and Sarnak, P. ``Chebyshev's Bias.'' Experimental Math. 3, 173-197, 1994. Selberg, A. and Erdös, P. ``An Elementary Proof of the Prime Number Theorem.'' Ann. Math. 50, 305-313, 1949. Shanks, D. ``The Prime Number Theorem.'' §1.6 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 15-17, 1993. Smith, D. E. A Source Book in Mathematics. New York: Dover, 1994. Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 25-35, 1991.
|
