Pólya Conjecture
Let 
be a Positive Integer and 
the number of (not necessarily distinct) Prime Factors of (with 
). Let 
be the number of Positive Integers 
with an Odd number ofPrime factors, and 
the number of Positive Integers with an Even number ofPrime factors. Pólya conjectured that
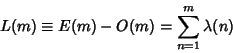
is
, where 
is the Liouville Function. The conjecture was made in 1919, and disproven by Haselgrove (1958) using a method due to Ingham (1942). Lehman(1960) found the first explicit counterexample, 
, and the smallest counterexample 
wasfound by Tanaka (1980). The first for which 
are 
, 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Tanaka 1980, Sloane's A028488). It is unknown if 
changes sign infinitely often (Tanaka 1980).
References
Haselgrove, C. B. ``A Disproof of a Conjecture of Pólya.'' Mathematika 5, 141-145, 1958. Ingham, A. E. ``On Two Conjectures in the Theory of Numbers.'' Amer. J. Math. 64, 313-319, 1942. Lehman, R. S. ``On Liouville's Function.'' Math. Comput. 14, 311-320, 1960. Sloane, N. J. A. Sequence A028488in ``The On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Tanaka, M. ``A Numerical Investigation on Cumulative Sum of the Liouville Function'' [sic]. Tokyo J. Math. 3, 187-189, 1980.
- Biquadratic Number
- Biquadratic Reciprocity Theorem
- Biquaternion
- Birational Transformation
- Birch Conjecture
- Birch-Swinnerton-Dyer Conjecture
- Birkhoff's Ergodic Theorem
- Birotunda
- Birthday Attack
- Birthday Problem
- Bisected Perimeter Point
- Bisection Procedure
- Bisector
- Bishop's Inequality
- Bishops Problem
- Bislit Cube
- Bispherical Coordinates
- Bitangent
- Bit Complexity
- Bivariate Distribution
- Bivector
- Biweight
- Blackman Function
- Black-Scholes Theory
- Black Spleenwort Fern