| 释义 |
QuaternionA member of a noncommutative Division Algebra first invented by William Rowan Hamilton.  The quaternions are sometimes also known as Hypercomplex Numbers and denoted The quaternions are sometimes also known as Hypercomplex Numbers and denoted  . While the quaternions are not commutative, they are associative. . While the quaternions are not commutative, they are associative.
The quaternions can be represented using complex 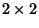 Matrices Matrices
 | (1) |
 and and  are Complex Numbers, are Complex Numbers,  , ,  , ,  , and , and  are Real, and are Real, and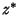 is the Complex Conjugate of is the Complex Conjugate of  . By analogy with the Complex Numbers being representableas a sum of Real and Imaginary Parts, . By analogy with the Complex Numbers being representableas a sum of Real and Imaginary Parts,  , a quaternion can also bewritten as a linear combination , a quaternion can also bewritten as a linear combination
 | (2) |
(Note that here, 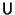 is used to denote the Identity Matrix, not is used to denote the Identity Matrix, not  .) The matrices are closely related tothe Pauli Spin Matrices .) The matrices are closely related tothe Pauli Spin Matrices  , , 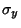 , , 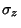 , combined with the Identity Matrix. From theabove definitions, it follows that , combined with the Identity Matrix. From theabove definitions, it follows that
Therefore  , , 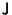 , and , and  are three essentially different solutions of the matrix equation are three essentially different solutions of the matrix equation
 | (10) |
In 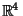 , the basis of the quaternions can be given by , the basis of the quaternions can be given by
The quaternions satisfy the following identities, sometimes known as Hamilton's Rules,
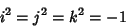 | (15) |
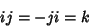 | (16) |
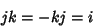 | (17) |
 | (18) |
The quaternions 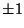 , ,  , , 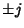 , and , and 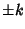 form a non-Abelian Group of order eight(with multiplication as the group operation) known as form a non-Abelian Group of order eight(with multiplication as the group operation) known as 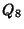 . .
The quaternions can be written in the form
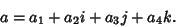 | (19) |
 | (20) |
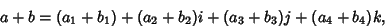 | (21) |
so the norm is
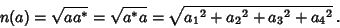 | (23) |
Quaternions can be interpreted as a Scalar plus a Vector by writing
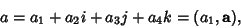 | (24) |
 . In this notation, quaternion multiplication has the particularly simpleform . In this notation, quaternion multiplication has the particularly simpleform
 | (25) |
 | (26) |
 | (27) |
A rotation about the Unit Vector 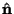 by an angle by an angle  can be computed using thequaternion can be computed using thequaternion
 | (28) |
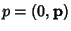 is then given by is then given by
 | (29) |
 . A concatenation of two rotations, first . A concatenation of two rotations, first  and then and then  , can be computed using the identity , can be computed using the identity
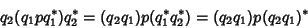 | (30) |
References
 Quaternions QuaternionsAltmann, S. L. Rotations, Quaternions, and Double Groups. Oxford, England: Clarendon Press, 1986. Arvo, J. Graphics Gems II. New York: Academic Press, pp. 351-354 and 377-380, 1994. Baker, A. L. Quaternions as the Result of Algebraic Operations. New York: Van Nostrand, 1911. Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Item 107, Feb. 1972. Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 230-234, 1996. Crowe, M. J. A History of Vector Analysis: The Evolution of the Idea of a Vectorial System. New York: Dover, 1994. Dickson, L. E. Algebras and Their Arithmetics. New York: Dover, 1960. Du Val, P. Homographies, Quaternions, and Rotations. Oxford, England: Oxford University Press, 1964. Ebbinghaus, H. D.; Hirzebruch, F.; Hermes, H.; Prestel, A; Koecher, M.; Mainzer, M.; and Remmert, R. Numbers. New York: Springer-Verlag, 1990. Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, p. 151, 1980. Hamilton, W. R. Lectures on Quaternions: Containing a Systematic Statement of a New Mathematical Method. Dublin: Hodges and Smith, 1853. Hamilton, W. R. Elements of Quaternions. London: Longmans, Green, 1866. Hamilton, W. R. The Mathematical Papers of Sir William Rowan Hamilton. Cambridge, England: Cambridge University Press, 1967. Hardy, A. S. Elements of Quaternions. Boston, MA: Ginn, Heath, & Co., 1881. Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Cambridge, England: Clarendon Press, 1965. Hearn, D. and Baker, M. P. Computer Graphics: C Version, 2nd ed. Englewood Cliffs, NJ: Prentice-Hall, pp. 419-420 and 617-618, 1996. Joly, C. J. A Manual of Quaternions. London: Macmillan, 1905. Julstrom, B. A. ``Using Real Quaternions to Represent Rotations in Three Dimensions.'' UMAP Modules in Undergraduate Mathematics and Its Applications, Module 652. Lexington, MA: COMAP, Inc., 1992. Kelland, P. and Tait, P. G. Introduction to Quaternions, 3rd ed. London: Macmillan, 1904. Nicholson, W. K. Introduction to Abstract Algebra. Boston, MA: PWS-Kent, 1993. Tait, P. G. An Elementary Treatise on Quaternions, 3rd ed., enl. Cambridge, England: Cambridge University Press, 1890. Tait, P. G. ``Quaternions.'' Encyclopædia Britannica, 9th ed. ca. 1886. ftp://ftp.netcom.com/pub/hb/hbaker/quaternion/tait/Encyc-Brit.ps.gz.
|
![]() The quaternions are sometimes also known as Hypercomplex Numbers and denoted
The quaternions are sometimes also known as Hypercomplex Numbers and denoted ![]() . While the quaternions are not commutative, they are associative.
. While the quaternions are not commutative, they are associative.![]() Matrices
Matrices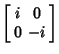
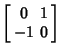

![]() , the basis of the quaternions can be given by
, the basis of the quaternions can be given by
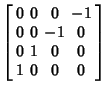

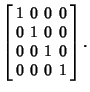
![]() ,
, ![]() ,
, ![]() , and
, and ![]() form a non-Abelian Group of order eight(with multiplication as the group operation) known as
form a non-Abelian Group of order eight(with multiplication as the group operation) known as ![]() .
.![]() by an angle
by an angle ![]() can be computed using thequaternion
can be computed using thequaternion![]() Quaternions
Quaternions