| 释义 |
Quintic EquationA general quintic cannot be solved algebraically in terms of finite additions, multiplications, and root extractions, asrigorously demonstrated by Abel  and Galois. and Galois. 
Euler  reduced the general quintic to reduced the general quintic to
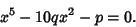 | (1) |
 | (2) |
 | (3) |
Consider the quintic
 | (4) |
 and and  and and  are Complex Numbers. This is called de Moivre's Quintic.Generalize it to are Complex Numbers. This is called de Moivre's Quintic.Generalize it to
 | (5) |
The  s satisfy s satisfy
Spearman and Williams (1994) show that an irreducible quintic
 | (17) |
 , ,  , and , and  such that such that
The Roots are then
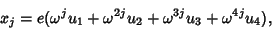 | (20) |
 |  |  | (21) | 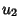 |  |  | (22) |  |  |  | (23) |  |  |  | (24) |  |  |  | (25) | 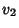 |  |  | (26) |  |  |  | (27) | 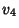 |  |  | (28) |  |  |  | (29) |
The general quintic can be solved in terms of Theta Functions, as was first done by Hermite in1858. Kronecker subsequently obtained the same solution more simply, and Brioshi also derived the equation. To do so, reducethe general quintic
 | (30) |
 | (31) |
where  is the Modulus, is the Modulus,  is the Parameter, and is the Parameter, and  is theNome. Solving is theNome. Solving
 | (36) |
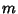 gives the inverse parameter gives the inverse parameter
 | (37) |
Felix Klein  used a Tschirnhausen Transformation to reduce the general quintic to the form used a Tschirnhausen Transformation to reduce the general quintic to the form
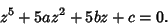 | (44) |
 | |  | | | (45) |
where  is a function of radicals of is a function of radicals of  , ,  , and , and  . The solution of this equation can be given in terms of Hypergeometric Functions as . The solution of this equation can be given in terms of Hypergeometric Functions as
 | (46) |
 | (47) |
then the Roots are
This technique gives closed form solutions in terms of Hypergeometric Functions in onevariable for any Polynomial equation which can be written in the form
 | (57) |
Cadenhad, Young, and Runge showed in 1885 that all irreducible solvable quintics with Coefficients of , ,  , and , and  missing have the following form missing have the following form
 | (58) |
 and and 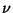 are Rational.See also Bring Quintic Form, Bring-Jerrard Quintic Form, Cubic Equation, de Moivre's Quintic,Principal Quintic Form, Quadratic Equation, Quartic Equation, Sextic Equation are Rational.See also Bring Quintic Form, Bring-Jerrard Quintic Form, Cubic Equation, de Moivre's Quintic,Principal Quintic Form, Quadratic Equation, Quartic Equation, Sextic Equation
ReferencesBirkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 3rd ed. New York: Macmillan, pp. 418-421, 1965.Chowla, S. ``On Quintic Equations Soluble by Radicals.'' Math. Student 13, 84, 1945. Cockle, J. ``Sketch of a Theory of Transcendental Roots.'' Phil. Mag. 20, 145-148, 1860. Cockle, J. `` On Transcendental and Algebraic Solution--Supplemental Paper.'' Phil. Mag. 13, 135-139, 1862. Davis, H. T. Introduction to Nonlinear Differential and Integral Equations. New York: Dover, p. 172, 1960. Dummit, D. S. ``Solving Solvable Quintics.'' Math. Comput. 57, 387-401, 1991. Glashan, J. C. ``Notes on the Quintic.'' Amer. J. Math. 8, 178-179, 1885. Harley, R. ``On the Solution of the Transcendental Solution of Algebraic Equations.'' Quart. J. Pure Appl. Math. 5, 337-361, 1862. Hermite, C. ``Sulla risoluzione delle equazioni del quinto grado.'' Annali di math. pura ed appl. 1, 256-259, 1858. King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996. King, R. B. and Cranfield, E. R. ``An Algorithm for Calculating the Roots of a General Quintic Equation from Its Coefficients.'' J. Math. Phys. 32, 823-825, 1991. Rosen, M. I. ``Niels Hendrik Abel and Equations of the Fifth Degree.'' Amer. Math. Monthly 102, 495-505, 1995. Shurman, J. Geometry of the Quintic. New York: Wiley, 1997. Spearman, B. K. and Williams, K. S. ``Characterization of Solvable Quintics  .'' Amer. Math. Monthly 101, 986-992, 1994. .'' Amer. Math. Monthly 101, 986-992, 1994. Young, G. P. ``Solution of Solvable Irreducible Quintic Equations, Without the Aid of a Resolvent Sextic.'' Amer. J. Math. 7, 170-177, 1885. |
![]() and Galois.
and Galois. ![]()
![]() reduced the general quintic to
reduced the general quintic to

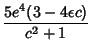












![]() used a Tschirnhausen Transformation to reduce the general quintic to the form
used a Tschirnhausen Transformation to reduce the general quintic to the form
![]() ,
, ![]() , and
, and ![]() missing have the following form
missing have the following form![]() .'' Amer. Math. Monthly 101, 986-992, 1994.
.'' Amer. Math. Monthly 101, 986-992, 1994.