| 释义 |
Ramanujan g- and G-FunctionsFollowing Ramanujan  (1913-14), write (1913-14), write
 | (1) |
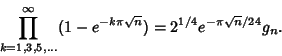 | (2) |
 and and 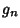 can be derived using the theory of Modular Functions and can always be expressedas roots of algebraic equations when can be derived using the theory of Modular Functions and can always be expressedas roots of algebraic equations when 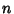 is Rational. For simplicity, Ramanujan tabulated is Rational. For simplicity, Ramanujan tabulated 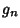 for for 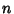 Even and Even and  for for 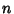 Odd. However, (6) allows Odd. However, (6) allows  and and 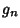 to be solved for in terms of to be solved for in terms of 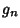 and and  ,giving ,giving
Using (3) and the above two equations allows 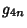 to be computed in terms of to be computed in terms of 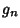 or or 
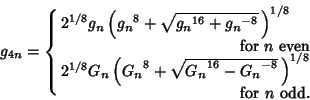 | (9) |
In terms of the Parameter  and complementary Parameter and complementary Parameter  , ,
Here,
 | (12) |
 for which for which
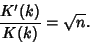 | (13) |
 gives gives
Analytic values for small values of 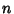 can be found in Ramanujan can be found in Ramanujan  (1913-1914) and Borwein and Borwein (1987),and have been compiled in Weisstein (1996). Ramanujan (1913-1914) and Borwein and Borwein (1987),and have been compiled in Weisstein (1996). Ramanujan  (1913-1914) contains a typographical error labeling (1913-1914) contains a typographical error labeling as as 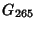 .See also G-Function .See also G-Function
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.Ramanujan, S. ``Modular Equations and Approximations to 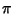 .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914. .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.  Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m. Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
|
![]() (1913-14), write
(1913-14), write
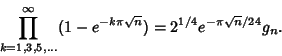
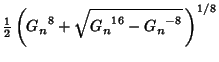
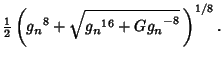
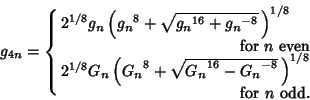
![]() and complementary Parameter
and complementary Parameter ![]() ,
,

![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.![]() Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.