Reflection Property
In the plane, the reflection property can be stated as three theorems (Ogilvy 1990, pp. 73-77):
- 1. The Locus of the center of a variable Circle, tangent to a fixed Circle and passing througha fixed point inside that Circle, is an Ellipse.
- 2. If a variable Circle is tangent to a fixed Circle and also passes through a fixed point outsidethe Circle, then the Locus of its moving center is a Hyperbola.
- 3. If a variable Circle is tangent to a fixed straight line and also passes through a fixed point not onthe line, then the Locus of its moving center is a Parabola.
Let ![]() be a smooth regular parameterized curve in
be a smooth regular parameterized curve in ![]() defined on an Open Interval
defined on an Open Interval ![]() , andlet
, andlet ![]() and
and ![]() be points in
be points in ![]() , where
, where ![]() is an
is an ![]() -D Projective Space. Then
-D Projective Space. Then![]() has a reflection property with Foci
has a reflection property with Foci ![]() and
and ![]() if, for each point
if, for each point ![]() ,
,
- 1. Any vector normal to the curve
 at
at 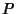 lies in the Span of the vectors
lies in the Span of the vectors and
and 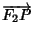 .
. - 2. The line normal to
 at
at 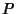 bisects one of the pairs of opposite Angles formed by theintersection of the lines joining
bisects one of the pairs of opposite Angles formed by theintersection of the lines joining  and
and 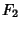 to
to 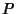 .
.
| Foci | Sign | Both foci finite | One focus finite | Both foci infinite |
| distinct | Positive | confocal ellipses | confocal parabolas | parallel lines |
| distinct | Negative | confocal hyperbola and perpendicular | confocal parabolas | parallel lines |
| bisector of interfoci line segment | ||||
| equal | concentric circles | parallel lines |
Let ![]() be a smooth connected surface, and let
be a smooth connected surface, and let ![]() and
and ![]() be points in
be points in ![]() , where
, where![]() is an
is an ![]() -D Projective Space. Then
-D Projective Space. Then ![]() has a reflection property with Foci
has a reflection property with Foci ![]() and
and![]() if, for each point
if, for each point ![]() ,
,
- 1. Any vector normal to
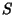 at
at 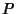 lies in the Span of the vectors
lies in the Span of the vectors  and
and 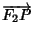 .
. - 2. The line normal to
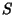 at
at 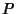 bisects one of the pairs of opposite angles formed by the intersection ofthe lines joining
bisects one of the pairs of opposite angles formed by the intersection ofthe lines joining  and
and 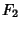 to
to 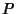 .
.
| Foci | Sign | Both foci finite | One focus finite | Both foci infinite |
| distinct | Positive | confocal ellipsoids | confocal paraboloids | parallel planes |
| distinct | Negative | confocal hyperboloids and plane perpendicular | confocal paraboloids | parallel planes |
| bisector of interfoci line segment | ||||
| equal | concentric spheres | parallel planes |
References
Drucker, D. ``Euclidean Hypersurfaces with Reflective Properties.'' Geometrica Dedicata 33, 325-329, 1990. Drucker, D. ``Reflective Euclidean Hypersurfaces.'' Geometrica Dedicata 39, 361-362, 1991. Drucker, D. ``Reflection Properties of Curves and Surfaces.'' Math. Mag. 65, 147-157, 1992. Drucker, D. and Locke, P. ``A Natural Classification of Curves and Surfaces with Reflection Properties.'' Math. Mag. 69, 249-256, 1996. Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 73-77, 1990. Wegner, B. ``Comment on `Euclidean Hypersurfaces with Reflective Properties'.'' Geometrica Dedicata 39, 357-359, 1991.
- Spence's Integral
- Sperner's Theorem
- Sphenocorona
- Sphenoid
- Sphenomegacorona
- Sphere
- Sphere-Cylinder Intersection
- Sphere Embedding
- Sphere Eversion
- Sphere Geodesic
- Sphere Packing
- Sphere Point Picking
- Sphere-Sphere Intersection
- Sphere with Tunnel
- Spherical Bessel Differential Equation
- Spherical Bessel Function
- Spherical Bessel Function of the First Kind
- Spherical Bessel Function of the Second Kind
- Spherical Bessel Function of the Third Kind
- Spherical Cap
- Spherical Coordinates
- Spherical Design
- Spherical Excess
- Spherical Frustum
- Spherical Geometry