Self-Avoiding Walk
N.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let the number of Random Walks on a ![]() -D lattice starting at the Origin which never land onthe same lattice point twice in
-D lattice starting at the Origin which never land onthe same lattice point twice in ![]() steps be denoted
steps be denoted ![]() . The first few values are
. The first few values are
| (1) | |||
| (2) | |||
| (3) |
The connective constant
| (4) |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) |
(Finch).
For the triangular lattice in the plane, ![]() (Alm 1993), and for the hexagonal planar lattice, it is conjectured that
(Alm 1993), and for the hexagonal planar lattice, it is conjectured that
| (10) |
The following limits are also believed to exist and to be Finite:
 | (11) |
 | (12) |
Define the mean square displacement over all ![]() -step self-avoiding walks
-step self-avoiding walks ![]() as
as
| (13) |
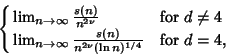 | (14) |
 | (15) |
References
Alm, S. E. ``Upper Bounds for the Connective Constant of Self-Avoiding Walks.'' Combin. Prob. Comput. 2, 115-136, 1993. Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/cnntv/cnntv.html Madras, N. and Slade, G. The Self-Avoiding Walk. Boston, MA: Birkhäuser, 1993.
- Arcsecant
- Arc Second
- Arcsine
- Arctangent
- Area
- Area Element
- Areal Coordinates
- Area-Preserving Map
- Area Principle
- Arf Invariant
- Argand Diagram
- Argand Plane
- Argoh's Conjecture
- Argument Addition Relation
- Argument (Complex Number)
- Argument (Elliptic Integral)
- Argument (Function)
- Argument Multiplication Relation
- Argument Principle
- Argument Variation
- Aristotle's Wheel Paradox
- Arithmetic
- Arithmetic-Geometric Mean
- Arithmetic Geometry
- Arithmetic-Harmonic Mean