Antoine's Necklace
Construct a chain 
of 
components in a solid Torus 
. Now form a chain 
of solid tori in , where
via inclusion. In each component of
, construct a smaller chain of solid tori embedded in that component.Denote the union of these smaller solid tori 
. Continue this process a countable number of times, then theintersection
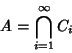
which is a nonempty compact Subset of
is called Antoine's necklace. Antoine's necklace is Homeomorphicwith the Cantor Set.See also Alexander's Horned Sphere, Necklace
References
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 73-74, 1976.
- Radical Integer
- Radical Line
- Radicand
- Radius
- Radius (Graph)
- Radius of Convergence
- Radius of Curvature
- Radius of Gyration
- Radius of Torsion
- Radius Vector
- Radix
- Radon-Nikodym Theorem
- Radon Transform
- Radon Transform--Cylinder
- Radon Transform--Delta Function
- Radon Transform--Gaussian
- Radon Transform--Square
- Rado's Sigma Function
- Railroad Track Problem
- Ramanujan 6-10-8 Identity
- Ramanujan Constant
- Ramanujan Continued Fraction
- Ramanujan Cos/Cosh Identity
- Ramanujan-Eisenstein Series
- Ramanujan Function