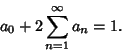| 释义 |
Apodization FunctionA function (also called a Tapering Function) used to bring an interferogram smoothly down to zero at the edges of thesampled region. This suppresses sidelobes which would otherwise be produced, but at the expense of widening the lines andtherefore decreasing the resolution.
The following are apodization functions for symmetrical (2-sided) interferograms, together with the InstrumentFunctions (or Apparatus Functions) they produce and a blowup of theInstrument Function sidelobes. The Instrument Function 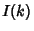 corresponding to a given apodization function corresponding to a given apodization function can be computed by taking the finite Fourier Cosine Transform, can be computed by taking the finite Fourier Cosine Transform,
 | (1) |
| Type | Apodization Function | Instrument Function | | Bartlett |  |  | | Blackman |  |  | | Connes |  |  | | Cosine |  |  | | Gaussian |  |  | | Hamming | 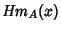 |  | | Hanning |  |  | | Uniform | 1 |  | | Welch |  |  |
where
 | 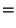 |  | (2) |  | 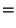 |  | (3) | | | | | (4) | 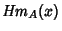 | 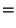 |  | (5) |  | 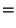 |  | (6) | 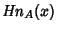 | 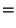 |  | (7) | | | 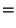 |  | (8) |  | 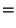 | 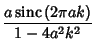 | (9) | | | 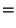 |  | (10) | 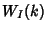 | 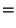 | 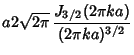 | (11) | | | 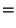 |  | (12) |
| Type | Instrument Function FWHM | IF Peak |  |  | | Bartlett | 1.77179 | 1 | 0.00000000 |  | | Blackman | 2.29880 | 0.84 |  | 0.00124325 | | Connes | 1.90416 |  | 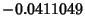 | 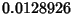 | | Cosine | 1.63941 |  |  |  | | Gaussian | -- | 1 | -- | -- | | Hamming | 1.81522 | 1.08 | 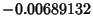 | 0.00734934 | | Hanning | 2.00000 | 1 |  | 0.00843441 | | Uniform | 1.20671 | 2 |  |  | | Welch | 1.59044 |  |  |  |
A general symmetric apodization function  can be written as a Fourier Series can be written as a Fourier Series
 | (13) |
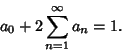 | (14) |
 | |  | (15) |
To obtain an Apodization Function with zero at 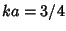 , use , use
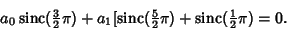 | (16) |
 | (17) |
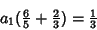 | (18) |
The Hamming Function is close to the requirement that the Apparatus Function goes to 0 at  , giving , giving
The Blackman Function is chosen so that the Apparatus Function goes to 0 at  and 9/4, giving and 9/4, giving
See also Bartlett Function, Blackman Function, Connes Function, Cosine Apodization Function,Full Width at Half Maximum,Gaussian Function, Hamming Function, Hann Function, Hanning Function, Mertz ApodizationFunction, Parzen Apodization Function, Uniform Apodization Function, Welch Apodization Function
References
Ball, J. A. ``The Spectral Resolution in a Correlator System'' §4.3.5 in Methods of Experimental Physics 12C (Ed. M. L. Meeks). New York: Academic Press, pp. 55-57, 1976.Blackman, R. B. and Tukey, J. W. ``Particular Pairs of Windows.'' In The Measurement of Power Spectra, From the Point of View of Communications Engineering. New York: Dover, pp. 95-101, 1959. Brault, J. W. ``Fourier Transform Spectrometry.'' In High Resolution in Astronomy: 15th Advanced Course of the Swiss Society of Astronomy and Astrophysics (Ed. A. Benz, M. Huber, and M. Mayor). Geneva Observatory, Sauverny, Switzerland, pp. 31-32, 1985. Harris, F. J. ``On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.'' Proc. IEEE 66, 51-83, 1978. Norton, R. H. and Beer, R. ``New Apodizing Functions for Fourier Spectroscopy.'' J. Opt. Soc. Amer. 66, 259-264, 1976. Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 547-548, 1992. Schnopper, H. W. and Thompson, R. I. ``Fourier Spectrometers.'' In Methods of Experimental Physics 12A (Ed. M. L. Meeks). New York: Academic Press, pp. 491-529, 1974. |
![]() corresponding to a given apodization function
corresponding to a given apodization function![]() can be computed by taking the finite Fourier Cosine Transform,
can be computed by taking the finite Fourier Cosine Transform,




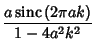
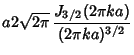

![]() can be written as a Fourier Series
can be written as a Fourier Series