Archimedean Solid
The Archimedean solids are convex Polyhedra which have a similar arrangement of nonintersectingregular plane Convex Polygons of two or more different types about each Vertex with all sides the same length. The Archimedean solids are distinguished from thePrisms, Antiprisms, and Elongated Square Gyrobicupola by their symmetry group:the Archimedean solids have a spherical symmetry, while the others have ``dihedral'' symmetry. The Archimedean solids aresometimes also referred to as the Semiregular Polyhedra.
Pugh (1976, p. 25) points out the Archimedean solids are all capable of being circumscribed by a regular Tetrahedron sothat four of their faces lie on the faces of that Tetrahedron. A method of constructing the Archimedean solids using amethod known as ``expansion'' has been enumerated by Stott (Stott 1910; Ball and Coxeter 1987, pp. 139-140).
Let the cyclic sequence ![]() represent the degrees of the faces surrounding a vertex (i.e.,
represent the degrees of the faces surrounding a vertex (i.e., ![]() is a list of the number of sides of all polygons surrounding any vertex). Then thedefinition of an Archimedean solid requires that the sequence must be the same for each vertex to within Rotationand Reflection. Walsh (1972) demonstrates that
is a list of the number of sides of all polygons surrounding any vertex). Then thedefinition of an Archimedean solid requires that the sequence must be the same for each vertex to within Rotationand Reflection. Walsh (1972) demonstrates that ![]() represents the degrees of the faces surrounding each vertex of asemiregular convex polyhedron or Tessellation of the plane Iff
represents the degrees of the faces surrounding each vertex of asemiregular convex polyhedron or Tessellation of the plane Iff
- 1.
 and every member of
and every member of 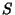 is at least 3,
is at least 3, - 2.
 , with equality in the case of a plane Tessellation, and
, with equality in the case of a plane Tessellation, and - 3. for every Odd Number
 ,
, 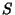 contains a subsequence (
contains a subsequence (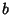 ,
,  ,
, 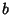 ).
).
Condition (1) simply says that the figure consists of two or more polygons, each having at least three sides. Condition (2)requires that the sum of interior angles at a vertex must be equal to a full rotation for the figure to lie in the plane,and less than a full rotation for a solid figure to be convex.
The usual way of enumerating the semiregular polyhedra is to eliminate solutions of conditions (1) and (2) using severalclasses of arguments and then prove that the solutions left are, in fact, semiregular (Kepler 1864, pp. 116-126; Catalan1865, pp. 25-32; Coxeter 1940, p. 394; Coxeter et al. 1954; Lines 1965, pp. 202-203; Walsh 1972). The following table gives all possible regular and semiregular polyhedra and tessellations. In the table, `P' denotes Platonic Solid,`M' denotes a Prism or Antiprism, `A' denotes an Archimedean solid, and `T' a plane tessellation.
| Figure | Solid | Schläfli Symbol | |
| (3, 3, 3) | P | Tetrahedron | |
| (3, 4, 4) | M | Triangular Prism | t |
| (3, 6, 6) | A | Truncated Tetrahedron | t |
| (3, 8, 8) | A | Truncated Cube | t |
| (3, 10, 10) | A | Truncated Dodecahedron | t |
| (3, 12, 12) | T | (Plane Tessellation) | t |
| (4, 4, | M | t | |
| (4, 4, 4) | P | Cube | |
| (4, 6, 6) | A | Truncated Octahedron | t |
| (4, 6, 8) | A | Great Rhombicuboctahedron | t |
| (4, 6, 10) | A | Great Rhombicosidodecahedron | t |
| (4, 6, 12) | T | (Plane Tessellation) | t |
| (4, 8, 8) | T | (Plane Tessellation) | t |
| (5, 5, 5) | P | Dodecahedron | |
| (5, 6, 6) | A | Truncated Icosahedron | t |
| (6, 6, 6) | T | (Plane Tessellation) | |
| (3, 3, 3, | M | s | |
| (3, 3, 3, 3) | P | Octahedron | |
| (3, 4, 3, 4) | A | Cuboctahedron | |
| (3, 5, 3, 5) | A | Icosidodecahedron | |
| (3, 6, 3, 6) | T | (Plane Tessellation) | |
| (3, 4, 4, 4) | A | Small Rhombicuboctahedron | r |
| (3, 4, 5, 4) | A | Small Rhombicosidodecahedron | r |
| (3, 4, 6, 4) | T | (Plane Tessellation) | r |
| (4, 4, 4, 4) | T | (Plane Tessellation) | |
| (3, 3, 3, 3, 3) | P | Icosahedron | |
| (3, 3, 3, 3, 4) | A | Snub Cube | s |
| (3, 3, 3, 3, 5) | A | Snub Dodecahedron | s |
| (3, 3, 3, 3, 6) | T | (Plane Tessellation) | s |
| (3, 3, 3, 4, 4) | T | (Plane Tessellation) | -- |
| (3, 3, 4, 3, 4) | T | (Plane Tessellation) | s |
| (3, 3, 3, 3, 3) | T | (Plane Tessellation) |
As shown in the above table, there are exactly 13 Archimedean solids (Walsh 1972, Ball and Coxeter 1987). They are calledthe Cuboctahedron, Great Rhombicosidodecahedron,Great Rhombicuboctahedron, Icosidodecahedron, SmallRhombicosidodecahedron, Small Rhombicuboctahedron, Snub Cube, Snub Dodecahedron, TruncatedCube, Truncated Dodecahedron, Truncated Icosahedron (soccer ball), Truncated Octahedron, andTruncated Tetrahedron. The Archimedean solids satisfy
where
Here are the Archimedean solids shown in alphabetical order (left to right, then continuing to the next row).
 |  |  | 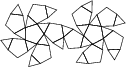 |
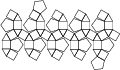 |  |  |  |
 | 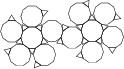 |  |  |
The following table lists the symbol and number of faces of each type for the Archimedean solids (Wenninger 1989, p. 9).
| Solid | Schläfli Symbol | Wythoff Symbol | C&R Symbol |
| Cuboctahedron | 2 | ||
| Great Rhombicosidodecahedron | t | 2 3 5 | |
| Great Rhombicuboctahedron | t | 2 3 4 | |
| Icosidodecahedron | 2 | ||
| Small Rhombicosidodecahedron | t | 3 5 | 3.4.5.4 |
| Small Rhombicuboctahedron | r | 3 4 | |
| Snub Cube | s | ||
| Snub Dodecahedron | s | ||
| Truncated Cube | t | 2 3 | |
| Truncated Dodecahedron | t | 2 3 | |
| Truncated Icosahedron | t | 2 5 | |
| Truncated Octahedron | t | 2 4 | |
| Truncated Tetrahedron | t | 2 3 |
| Solid | ||||||||
| Cuboctahedron | 12 | 24 | 8 | 6 | ||||
| Great Rhombicosidodecahedron | 120 | 180 | 30 | 20 | 12 | |||
| Great Rhombicuboctahedron | 48 | 72 | 12 | 8 | 6 | |||
| Icosidodecahedron | 30 | 60 | 20 | 12 | ||||
| Small Rhombicosidodecahedron | 60 | 120 | 20 | 30 | 12 | |||
| Small Rhombicuboctahedron | 24 | 48 | 8 | 18 | ||||
| Snub Cube | 24 | 60 | 32 | 6 | ||||
| Snub Dodecahedron | 60 | 150 | 80 | 12 | ||||
| Truncated Cube | 24 | 36 | 8 | 6 | ||||
| Truncated Dodecahedron | 60 | 90 | 20 | 12 | ||||
| Truncated Icosahedron | 60 | 90 | 12 | 20 | ||||
| Truncated Octahedron | 24 | 36 | 6 | 8 | ||||
| Truncated Tetrahedron | 12 | 18 | 4 | 4 |
Let ![]() be the Inradius,
be the Inradius, ![]() the Midradius, and
the Midradius, and ![]() the Circumradius. The following tablesgive the analytic and numerical values of
the Circumradius. The following tablesgive the analytic and numerical values of ![]() ,
, ![]() , and
, and ![]() for the Archimedean solids with Edges of unit length.
for the Archimedean solids with Edges of unit length.
| Solid | |||
| Cuboctahedron | 1 | ||
| Great Rhombicosidodecahedron | |||
| Great Rhombicuboctahedron | |||
| Icosidodecahedron | |||
| Small Rhombicosidodecahedron | |||
| Small Rhombicuboctahedron | |||
| Snub Cube | * | * | * |
| Snub Dodecahedron | * | * | * |
| Truncated Cube | |||
| Truncated Dodecahedron | |||
| Truncated Icosahedron | |||
| Truncated Octahedron | |||
| Truncated Tetrahedron |
| Solid | |||
| Cuboctahedron | 0.75 | 0.86603 | 1 |
| Great Rhombicosidodecahedron | 3.73665 | 3.76938 | 3.80239 |
| Great Rhombicuboctahedron | 2.20974 | 2.26303 | 2.31761 |
| Icosidodecahedron | 1.46353 | 1.53884 | 1.61803 |
| Small Rhombicosidodecahedron | 2.12099 | 2.17625 | 2.23295 |
| Small Rhombicuboctahedron | 1.22026 | 1.30656 | 1.39897 |
| Snub Cube | 1.15763 | 1.24719 | 1.34371 |
| Snub Dodecahedron | 2.03969 | 2.09688 | 2.15583 |
| Truncated Cube | 1.63828 | 1.70711 | 1.77882 |
| Truncated Dodecahedron | 2.88526 | 2.92705 | 2.96945 |
| Truncated Icosahedron | 2.37713 | 2.42705 | 2.47802 |
| Truncated Octahedron | 1.42302 | 1.5 | 1.58114 |
| Truncated Tetrahedron | 0.95940 | 1.06066 | 1.17260 |
The Duals of the Archimedean solids, sometimes called the Catalan Solids, are given in the following table.
| Archimedean Solid | Dual |
| Cuboctahedron | Rhombic Dodecahedron |
| Great Rhombicosidodecahedron | Disdyakis Triacontahedron |
| Great Rhombicuboctahedron | Disdyakis Dodecahedron |
| Icosidodecahedron | Rhombic Triacontahedron |
| Small Rhombicosidodecahedron | Deltoidal Hexecontahedron |
| Small Rhombicuboctahedron | Deltoidal Icositetrahedron |
| Snub Dodecahedron (laevo) | Pentagonal Hexecontahedron (dextro) |
| Snub Cube (laevo) | Pentagonal Icositetrahedron (dextro) |
| Truncated Cube | Small Triakis Octahedron |
| Truncated Dodecahedron | Triakis Icosahedron |
| Truncated Icosahedron | Pentakis Dodecahedron |
| Truncated Octahedron | Tetrakis Hexahedron |
| Truncated Tetrahedron | Triakis Tetrahedron |
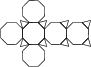
Here are the Archimedean Duals (Holden 1971, Pearce 1978) displayed in alphabetical order (left toright, then continuing to the next row).
Here are the Archimedean solids paired with their Duals.
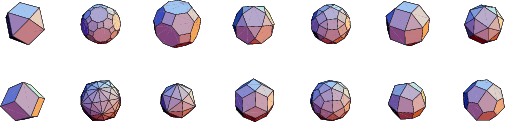
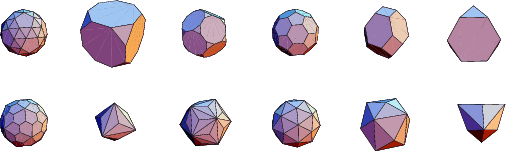
The Archimedean solids and their Duals are all Canonical Polyhedra.
See also Archimedean Solid Stellation, Catalan Solid, Deltahedron, Johnson Solid, Kepler-PoinsotSolid, Platonic Solid, Semiregular Polyhedron, Uniform Polyhedron
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 136, 1987. Behnke, H.; Bachman, F.; Fladt, K.; and Kunle, H. (Eds.). Fundamentals of Mathematics, Vol. 2. Cambridge, MA: MIT Press, pp. 269-286, 1974. Catalan, E. ``Mémoire sur la Théorie des Polyèdres.'' J. l'École Polytechnique (Paris) 41, 1-71, 1865. Coxeter, H. S. M. ``The Pure Archimedean Polytopes in Six and Seven Dimensions.'' Proc. Cambridge Phil. Soc. 24, 1-9, 1928. Coxeter, H. S. M. ``Regular and Semi-Regular Polytopes I.'' Math. Z. 46, 380-407, 1940. Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. ``Uniform Polyhedra.'' Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954. Critchlow, K. Order in Space: A Design Source Book. New York: Viking Press, 1970. Cromwell, P. R. Polyhedra. New York: Cambridge University Press, pp. 79-86, 1997. Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., 1989. Holden, A. Shapes, Space, and Symmetry. New York: Dover, p. 54, 1991. Kepler, J. ``Harmonice Mundi.'' Opera Omnia, Vol. 5. Frankfurt, pp. 75-334, 1864. Kraitchik, M. Mathematical Recreations. New York: W. W. Norton, pp. 199-207, 1942. Pearce, P. Structure in Nature is a Strategy for Design. Cambridge, MA: MIT Press, pp. 34-35, 1978. Pugh, A. Polyhedra: A Visual Approach. Berkeley: University of California Press, p. 25, 1976. Rawles, B. A. ``Platonic and Archimedean Solids--Faces, Edges, Areas, Vertices, Angles, Volumes, Sphere Ratios.'' http://www.intent.com/sg/polyhedra.html. Rorres, C. ``Archimedean Solids: Pappus.'' http://www.mcs.drexel.edu/~crorres/Archimedes/Solids/Pappus.html. Steinitz, E. and Rademacher, H. Vorlesungen über die Theorie der Polyheder. Berlin, p. 11, 1934. Stott, A. B. Verhandelingen der Koninklijke Akad. Wetenschappen, Amsterdam 11, 1910. Walsh, T. R. S. ``Characterizing the Vertex Neighbourhoods of Semi-Regular Polyhedra.'' Geometriae Dedicata 1, 117-123, 1972. Wenninger, M. J. Polyhedron Models. New York: Cambridge University Press, 1989.
- Sorites Paradox
- Sorting
- Sort-Then-Add Sequence
- Source
- Sous-Double
- Souslin Set
- Souslin's Hypothesis
- Sous-Triple
- Space
- Space Conic
- Space Curve
- Space Diagonal
- Space Distance
- Space Division
- Space-Filling Curve
- Space-Filling Function
- Space-Filling Polyhedron
- Space Groups
- Space of Closed Paths
- Span (Geometry)
- Span (Link)
- Span (Polynomial)
- Span (Set)
- Span (Vectors)
- Sparse Matrix