| 释义 |
Arnold's Cat MapThe best known example of an Anosov Diffeomorphism. It is given by the Transformation
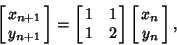 | (1) |
 and and 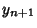 are computed mod 1. The Arnold cat mapping is non-Hamiltonian, nonanalytic, and mixing. However, it is Area-Preserving since the Determinant is 1. The LyapunovCharacteristic Exponents are given by are computed mod 1. The Arnold cat mapping is non-Hamiltonian, nonanalytic, and mixing. However, it is Area-Preserving since the Determinant is 1. The LyapunovCharacteristic Exponents are given by
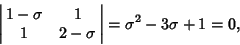 | (2) |
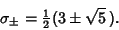 | (3) |
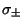 into the Matrix Equation into the Matrix Equation
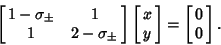 | (4) |
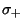 , the solution is , the solution is
 | (5) |
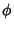 is the Golden Ratio, so the unstable (normalized) Eigenvector is is the Golden Ratio, so the unstable (normalized) Eigenvector is
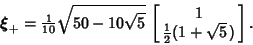 | (6) |
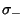 , the solution is , the solution is
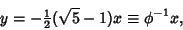 | (7) |
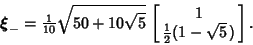 | (8) |
|