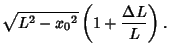| 释义 |
AstroidA 4-cusped Hypocycloid which is sometimes also called a Tetracuspid, Cubocycloid, or Paracycle.The parametric equations of the astroid can be obtained by plugging in  or or  into the equations for ageneral Hypocycloid, giving into the equations for ageneral Hypocycloid, giving
In Cartesian Coordinates,
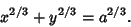 | (3) |
 | (4) |
The Arc Length, Curvature, and Tangential Angle are
As usual, care must be taken in the evaluation of  for for  . Since (5) comes from an integral involving theAbsolute Value of a function, it must be monotonic increasing. Each Quadrant can be treated correctly bydefining . Since (5) comes from an integral involving theAbsolute Value of a function, it must be monotonic increasing. Each Quadrant can be treated correctly bydefining
 | (8) |
 is the Floor Function, giving the formula is the Floor Function, giving the formula
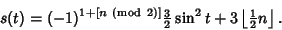 | (9) |
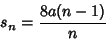 | (10) |
 , ,
 | (11) |
 | (12) |
 , ,
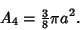 | (13) |
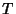 fromthe point with parameter fromthe point with parameter  is is  . The equation of this Tangent . The equation of this Tangent 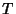 is is
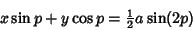 | (14) |
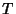 cut the x-Axis and the y-Axis at cut the x-Axis and the y-Axis at  and and  , respectively. Then the length , respectively. Then the length  is a constantand is equal to is a constantand is equal to 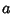 . .
The astroid can also be formed as the Envelope produced when a Line Segment is moved with each end on one of apair of Perpendicular axes (e.g., it is the curve enveloped by a ladder sliding against a wall or a garage door with thetop corner moving along a vertical track; left figure above). The astroid is therefore a Glissette. To see this, notethat for a ladder of length 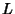 , the points of contact with the wall and floor are , the points of contact with the wall and floor are  and and  ,respectively. The equation of the Line made by the ladder with its foot at ,respectively. The equation of the Line made by the ladder with its foot at  is therefore is therefore
 | (15) |
 | (16) |
 | (17) |
Noting that
allows this to be written implicitly as
 | (22) |
The related problem obtained by having the ``garage door'' of length 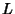 with an ``extension'' of length with an ``extension'' of length 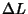 move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''end for the foot of the door at horizontal position move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''end for the foot of the door at horizontal position  and Angle and Angle 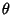 is given by is given by
Using
 | (25) |
Solving (26) for  , plugging into (27) and squaring then gives , plugging into (27) and squaring then gives
 | (28) |
 | (29) |
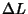 and and  . .
The astroid is also the Envelope of the family of Ellipses
 | (30) |
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 172-175, 1972.Lee, X. ``Astroid.''http://www.best.com/~xah/SpecialPlaneCurves_dir/Astroid_dir/astroid.html. Lockwood, E. H. ``The Astroid.'' Ch. 6 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 52-61, 1967. MacTutor History of Mathematics Archive. ``Astroid.''http://www-groups.dcs.st-and.ac.uk/~history/Curves/Astroid.html. Yates, R. C. ``Astroid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 1-3, 1952. |

![]() or
or ![]() into the equations for ageneral Hypocycloid, giving
into the equations for ageneral Hypocycloid, giving

![]() , the points of contact with the wall and floor are
, the points of contact with the wall and floor are ![]() and
and ![]() ,respectively. The equation of the Line made by the ladder with its foot at
,respectively. The equation of the Line made by the ladder with its foot at ![]() is therefore
is therefore
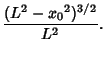
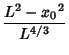

![]() with an ``extension'' of length
with an ``extension'' of length ![]() move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''end for the foot of the door at horizontal position
move up and down a slotted track also gives a surprising answer. In this case, the position of the ``extended''end for the foot of the door at horizontal position ![]() and Angle
and Angle ![]() is given by
is given by