| 释义 |
Bessel Function of the Second KindA Bessel function of the second kind 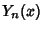 is a solution to the Bessel Differential Equation which is singular at theorigin. Bessel functions of the second kind are also called Neumann Functions or WeberFunctions. The above plot shows is a solution to the Bessel Differential Equation which is singular at theorigin. Bessel functions of the second kind are also called Neumann Functions or WeberFunctions. The above plot shows 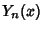 for for  , 2, ..., 5. , 2, ..., 5.
Let  be the first solution and be the first solution and 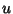 be the other one (since the Bessel Differential Equation issecond-order, there are two Linearly Independent solutions). Then be the other one (since the Bessel Differential Equation issecond-order, there are two Linearly Independent solutions). Then
 | (1) |
 | (2) |
 (1) minus (1) minus  (2), (2),
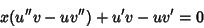 | (3) |
 | (4) |
 , where , where 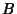 is a constant. Divide by is a constant. Divide by  , ,
 | (5) |
 | (6) |
 gives gives
where the Bessel function of the second kind is defined by , 1, 2, ..., , 1, 2, ...,  is the Euler-Mascheroni Constant, and is the Euler-Mascheroni Constant, and
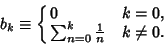 | (9) |
 | (10) |
Asymptotic equations are
where 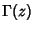 is a Gamma Function.See also Bessel Function of the First Kind, Bourget's Hypothesis, Hankel Function is a Gamma Function.See also Bessel Function of the First Kind, Bourget's Hypothesis, Hankel Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bessel Functions  and and 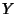 .'' §9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972. .'' §9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972.Arfken, G. ``Neumann Functions, Bessel Functions of the Second Kind,  .'' §11.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985. .'' §11.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985. Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 625-627, 1953. Spanier, J. and Oldham, K. B. ``The Neumann Function  .'' Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987. .'' Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987.
|

![]() is a solution to the Bessel Differential Equation which is singular at theorigin. Bessel functions of the second kind are also called Neumann Functions or WeberFunctions. The above plot shows
is a solution to the Bessel Differential Equation which is singular at theorigin. Bessel functions of the second kind are also called Neumann Functions or WeberFunctions. The above plot shows ![]() for
for ![]() , 2, ..., 5.
, 2, ..., 5.![]() be the first solution and
be the first solution and ![]() be the other one (since the Bessel Differential Equation issecond-order, there are two Linearly Independent solutions). Then
be the other one (since the Bessel Differential Equation issecond-order, there are two Linearly Independent solutions). Then


![]() and
and ![]() .'' §9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972.
.'' §9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 358-364, 1972.![]() .'' §11.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985.
.'' §11.3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 596-604, 1985.![]() .'' Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987.
.'' Ch. 54 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 533-542, 1987.