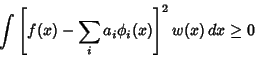| 释义 |
Bessel's InequalityIf 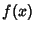 is piecewise Continuous and has a general Fourier Series is piecewise Continuous and has a general Fourier Series
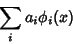 | (1) |
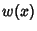 , it must be true that , it must be true that
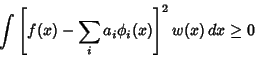 | (2) |
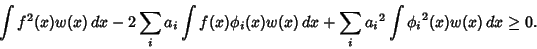 | (3) |
 | (4) |
 | (5) |
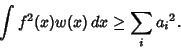 | (6) |
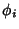 are not Complete. If they areComplete, then the inequality (2) becomes an equality, so (6) becomes anequality and is known as Parseval's Theorem. If are not Complete. If they areComplete, then the inequality (2) becomes an equality, so (6) becomes anequality and is known as Parseval's Theorem. If 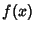 has a simple Fourier Series expansion withCoefficients has a simple Fourier Series expansion withCoefficients  , , 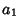 , ,  , ,  and and  , ..., , ..., 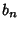 , then , then
 | (7) |
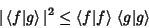 | (8) |
 in a superposition of Eigenfunctions of in a superposition of Eigenfunctions of  , ,  . Then . Then
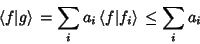 | (9) |
 | (10) |
 is normalized, then is normalized, then 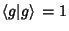 and and
 | (11) |
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 526-527, 1985.Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA: Academic Press, p. 1102, 1980.
|
![]() is piecewise Continuous and has a general Fourier Series
is piecewise Continuous and has a general Fourier Series