| 释义 |
Birthday ProblemConsider the probability  that no two people out of a group of that no two people out of a group of 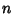 will have matching birthdays out of will have matching birthdays out of  equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person'sbirthday is different is equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person'sbirthday is different is  , that the third person's birthday is different from the first two is , that the third person's birthday is different from the first two is  ,and so on, up through the ,and so on, up through the 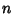 th person. Explicitly, th person. Explicitly,
But this can be written in terms of Factorials as
 | (2) |
 that two people out of a group of that two people out of a group of 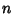 do have the same birthday is therefore do have the same birthday is therefore
 | (3) |
 is ignored, then the number ofpeople needed for there to be at least a 50% chance that two share birthdays is the smallest is ignored, then the number ofpeople needed for there to be at least a 50% chance that two share birthdays is the smallest 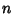 such that such that . This is given by . This is given by  , since , since
The number 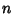 of people needed to obtain of people needed to obtain 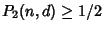 for for  , 2, ..., are 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, ...(Sloane's A033810). , 2, ..., are 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, ...(Sloane's A033810).
The probability  can be estimated as can be estimated as
where the latter has error
 | (7) |
In general, let  denote the probability that a birthday is shared by exactly denote the probability that a birthday is shared by exactly 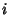 (and no more) people out of a group of (and no more) people out of a group of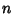 people. Then the probability that a birthday is shared by people. Then the probability that a birthday is shared by  or more people is given by or more people is given by
 | (8) |
 can be computed explicitly as can be computed explicitly as
where  is a Binomial Coefficient, is a Binomial Coefficient,  is a Gamma Function, and is a Gamma Function, and  is an Ultraspherical Polynomial. This gives the explicit formula for is an Ultraspherical Polynomial. This gives the explicit formula for  as as
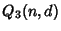 cannot be computed in entirely closed form, but a partially reduced form is cannot be computed in entirely closed form, but a partially reduced form is | |  | | | (11) |
where | | | (12) |
and  is a Generalized Hypergeometric Function. is a Generalized Hypergeometric Function.
In general,  can be computed using the Recurrence Relation can be computed using the Recurrence Relation
 | (13) |
 and so rapidly becomes unwieldy.The minimal number of people to give a 50% probability of having at least and so rapidly becomes unwieldy.The minimal number of people to give a 50% probability of having at least 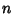 coincident birthdays is 1, 23, 88,187, 313, 460, 623, 798, 985, 1181, 1385, 1596, 1813, ... (Sloane's A014088; Diaconis and Mosteller 1989). coincident birthdays is 1, 23, 88,187, 313, 460, 623, 798, 985, 1181, 1385, 1596, 1813, ... (Sloane's A014088; Diaconis and Mosteller 1989).
A good approximation to the number of people 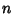 such that such that  is some given value can be given by solving the equation is some given value can be given by solving the equation
 | (14) |
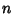 and taking and taking , where , where  is the Ceiling Function (Diaconis and Mosteller 1989). For is the Ceiling Function (Diaconis and Mosteller 1989). For  and and  , 2, 3,..., this formula gives , 2, 3,..., this formula gives 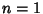 , 23, 88, 187, 313, 459, 722, 797, 983, 1179, 1382, 1592, 1809, ..., which differ from thetrue values by from 0 to 4. A much simpler but also poorer approximation for , 23, 88, 187, 313, 459, 722, 797, 983, 1179, 1382, 1592, 1809, ..., which differ from thetrue values by from 0 to 4. A much simpler but also poorer approximation for 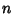 such that such that  for for  is given by is given by
 | (15) |
 , 4, .... , 4, ....
The ``almost'' birthday problem, which asks the number of people needed such that two have a birthday within a day of each other,was considered by Abramson and Moser (1970), who showed that 14 people suffice. An approximation for the minimum number ofpeople needed to get a 50-50 chance that two have a match within  days out of days out of  possible is given by possible is given by
 | (16) |
References
Abramson, M. and Moser, W. O. J. ``More Birthday Surprises.'' Amer. Math. Monthly 77, 856-858, 1970.Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 45-46, 1987. Bloom, D. M. ``A Birthday Problem.'' Amer. Math. Monthly 80, 1141-1142, 1973. Bogomolny, A. ``Coincidence.'' http://www.cut-the-knot.com/do_you_know/coincidence.html. Clevenson, M. L. and Watkins, W. ``Majorization and the Birthday Inequality.'' Math. Mag. 64, 183-188, 1991. Diaconis, P. and Mosteller, F. ``Methods of Studying Coincidences.'' J. Amer. Statist. Assoc. 84, 853-861, 1989. Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 31-32, 1968. Finch, S. ``Puzzle #28 [June 1997]: Coincident Birthdays.'' http://www.mathsoft.com/mathcad/library/puzzle/soln28/soln28.html. Gehan, E. A. ``Note on the `Birthday Problem.''' Amer. Stat. 22, 28, Apr. 1968. Heuer, G. A. ``Estimation in a Certain Probability Problem.'' Amer. Math. Monthly 66, 704-706, 1959. Hocking, R. L. and Schwertman, N. C. ``An Extension of the Birthday Problem to Exactly  Matches.'' College Math. J. 17, 315-321, 1986. Matches.'' College Math. J. 17, 315-321, 1986. Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 102-103, 1975. Klamkin, M. S. and Newman, D. J. ``Extensions of the Birthday Surprise.'' J. Combin. Th. 3, 279-282, 1967. Levin, B. ``A Representation for Multinomial Cumulative Distribution Functions.'' Ann. Statistics 9, 1123-1126, 1981. McKinney, E. H. ``Generalized Birthday Problem.'' Amer. Math. Monthly 73, 385-387, 1966. Mises, R. von. ``Über Aufteilungs--und Besetzungs-Wahrscheinlichkeiten.'' Revue de la Faculté des Sciences de l'Université d'Istanbul, N. S. 4, 145-163, 1939. Reprinted in Selected Papers of Richard von Mises, Vol. 2 (Ed. P. Frank, S. Goldstein, M. Kac, W. Prager, G. Szegö, and G. Birkhoff). Providence, RI: Amer. Math. Soc., pp. 313-334, 1964. Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 179-180, 1994. Sayrafiezadeh, M. ``The Birthday Problem Revisited.'' Math. Mag. 67, 220-223, 1994. Sevast'yanov, B. A. ``Poisson Limit Law for a Scheme of Sums of Dependent Random Variables.'' Th. Prob. Appl. 17, 695-699, 1972. Sloane, N. J. A.A014088 andA033810 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Stewart, I. ``What a Coincidence!'' Sci. Amer. 278, 95-96, June 1998. Tesler, L. ``Not a Coincidence!'' http://www.nomodes.com/coincidence.html.
|
![]() that no two people out of a group of
that no two people out of a group of ![]() will have matching birthdays out of
will have matching birthdays out of ![]() equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person'sbirthday is different is
equally possible birthdays. Start with an arbitrary person's birthday, then note that the probability that the second person'sbirthday is different is ![]() , that the third person's birthday is different from the first two is
, that the third person's birthday is different from the first two is ![]() ,and so on, up through the
,and so on, up through the ![]() th person. Explicitly,
th person. Explicitly,

![]() can be estimated as
can be estimated as

![]() denote the probability that a birthday is shared by exactly
denote the probability that a birthday is shared by exactly ![]() (and no more) people out of a group of
(and no more) people out of a group of![]() people. Then the probability that a birthday is shared by
people. Then the probability that a birthday is shared by ![]() or more people is given by
or more people is given by



![]() is a Binomial Coefficient,
is a Binomial Coefficient, ![]() is a Gamma Function, and
is a Gamma Function, and ![]() is an Ultraspherical Polynomial. This gives the explicit formula for
is an Ultraspherical Polynomial. This gives the explicit formula for ![]() as
as



![]() can be computed using the Recurrence Relation
can be computed using the Recurrence Relation
![]() such that
such that ![]() is some given value can be given by solving the equation
is some given value can be given by solving the equation![]() days out of
days out of ![]() possible is given by
possible is given by![]() Matches.'' College Math. J. 17, 315-321, 1986.
Matches.'' College Math. J. 17, 315-321, 1986.