“Bishops Problem”的概念、定义、习题解题方法及翻译-数学辞典

单词

Bishops Problem

释义

Bishops Problem

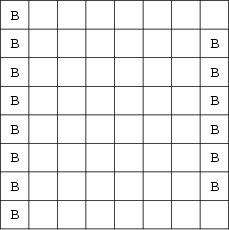
Find the maximum number of bishops which can be placed on an Chessboard such that no two attack eachother. The answer is (Dudeney 1970, Madachy 1979), giving the sequence 2, 4, 6, 8, ... (the EvenNumbers) for , 3, .... One maximal solution for is illustrated above. The number of distinctmaximal arrangements of bishops for , 2, ... are 1, 4, 26, 260, 3368, ... (Sloane's A002465). The number ofrotationally and reflectively distinct solutions on an board for is

(Dudeney 1970, p. 96; Madachy 1979, p. 45; Pickover 1995). An equivalent formula is

where

is the Floor Function,giving the sequence for

, 2, ... as 1, 1, 2, 3, 6, 10, 20, 36, ... (Sloane's A005418).

The minimum number of bishops needed to occupy or attack all squares on an Chessboard is , arrangedas illustrated above.

See also Chess, Kings Problem, Knights Problem, Queens Problem, Rooks Problem

References

Ahrens, W. Mathematische Unterhaltungen und Spiele, Vol. 1, 3rd ed. Leipzig, Germany: Teubner, p. 271, 1921.

Dudeney, H. E. ``Bishops--Unguarded'' and ``Bishops--Guarded.'' §297 and 298 in Amusements in Mathematics. New York: Dover, pp. 88-89, 1970.

Guy, R. K. ``The Queens Problem.'' §C18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 133-135, 1994.

Madachy, J. Madachy's Mathematical Recreations. New York: Dover, pp. 36-46, 1979.

Pickover, C. A. Keys to Infinity. New York: Wiley, pp. 74-75, 1995.

Sloane, N. J. A. SequencesA002465/M3616and A005418/M0771in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。