Blancmange Function
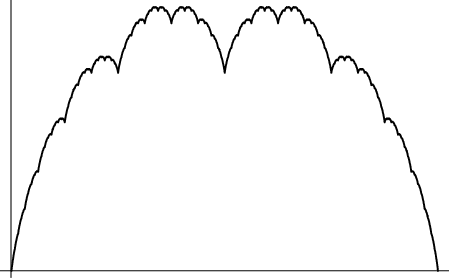
A Continuous Function which is nowhere Differentiable. The iterations towards the continuous function areBatrachions resembling the Hofstadter-Conway $10,000 Sequence. The first six iterations areillustrated below. The 
th iteration contains 
points, where 
, and can be obtained by setting
, letting
and looping over
to 1 by steps of 
and 
to 
by steps of 
.
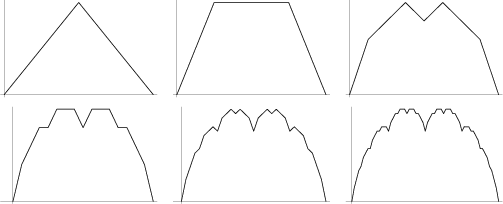
Peitgen and Saupe (1988) refer to this curve as the Takagi Fractal Curve.
See also Hofstadter-Conway $10,000 Sequence, Weierstraß Function
References
Dixon, R. Mathographics. New York: Dover, pp. 175-176 and 210, 1991. Peitgen, H.-O. and Saupe, D. (Eds.). ``Midpoint Displacement and Systematic Fractals: The Takagi Fractal Curve, Its Kin, and the Related Systems.'' §A.1.2 in The Science of Fractal Images. New York: Springer-Verlag, pp. 246-248, 1988. Takagi, T. ``A Simple Example of the Continuous Function without Derivative.'' Proc. Phys. Math. Japan 1, 176-177, 1903. Tall, D. O. ``The Blancmange Function, Continuous Everywhere but Differentiable Nowhere.'' Math. Gaz. 66, 11-22, 1982. Tall, D. ``The Gradient of a Graph.'' Math. Teaching 111, 48-52, 1985.
- Midpoint
- Midpoint Ellipse
- Midradius
- Midrange
- Midsphere
- Midy's Theorem
- Mikusinski's Problem
- Milin Conjecture
- Mill
- Miller-Askinuze Solid
- Miller Cylindrical Projection
- Miller's Algorithm
- Miller's Primality Test
- Miller's Solid
- Milliard
- Millin Series
- Million
- Mills' Constant
- Milne's Method
- Milnor's Conjecture
- Milnor's Theorem
- Minimal Cover
- Minimal Discriminant
- Minimal Matrix
- Minimal Residue