B-Spline
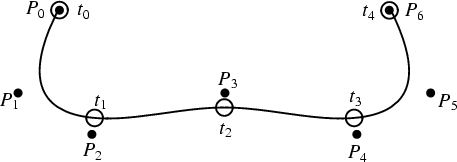
A generalization of the Bézier Curve. Let a vector known as the Knot Vector bedefined
 | (1) |
is a nondecreasing Sequence with 
, and define control points 
, ...,
. Define the degree as | (2) |
, ..., 
are called Internal Knots.Define the basis functions as
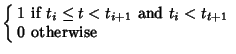 |  |  | (3) |
 | |  | |
| (4) |
Then the curve defined by
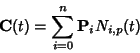 | (5) |
knots equal 0 and last equal to 1) anduniform B-spline (Internal Knots are equally spaced). A B-Spline with no InternalKnots is a Bézier Curve.The degree of a B-spline is independent of the number of control points, so a low order can always be maintained forpurposes of numerical stability. Also, a curve is 
times differentiable at a point where 
duplicate knotvalues occur. The knot values determine the extent of the control of the control points.
- Wave Surface
- Weak Convergence
- Weak Law of Large Numbers
- Weakly Binary Tree
- Weakly Complete Sequence
- Weakly Independent
- Weakly Triple-Free Set
- Weber Differential Equations
- Weber Functions
- Weber's Discontinuous Integrals
- Weber's Formula
- Weber-Sonine Formula
- Weber's Theorem
- Web Graph
- Wedderburn's Theorem
- Weddle's Rule
- Wedge
- Wedge Product
- Weekday
- Weibull Distribution
- Weierstrass M-Test
- Weierstraß Approximation Theorem
- Weierstraß-Casorati Theorem
- Weierstraß Constant
- Weierstraß Elliptic Function