| 释义 |
Snedecor's F-DistributionIf a random variable  has a Chi-Squared Distribution with has a Chi-Squared Distribution with  degrees of freedom ( degrees of freedom ( ) and a random variable ) and a random variable 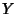 has a Chi-Squared Distribution with has a Chi-Squared Distribution with 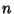 degrees of freedom ( degrees of freedom ( ), and ), and  and and 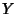 are independent, then are independent, then
 | (1) |
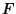 -distribution with -distribution with  and and 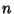 degrees of freedom degrees of freedom
 | (2) |
 . The Moments about 0 are . The Moments about 0 are
so the Moments about the Mean are given by
where
 | (10) |
where
 | (15) |
 | (16) |
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 536, 1987.
|
![]() has a Chi-Squared Distribution with
has a Chi-Squared Distribution with ![]() degrees of freedom (
degrees of freedom (![]() ) and a random variable
) and a random variable ![]() has a Chi-Squared Distribution with
has a Chi-Squared Distribution with ![]() degrees of freedom (
degrees of freedom (![]() ), and
), and ![]() and
and ![]() are independent, then
are independent, then









