Sphere Packing

Let denote the Packing Density, which is the fraction of a Volume filled by identical packedSpheres. In 2-D (Circle Packing), there are two periodic packings for identicalCircles: square lattice and hexagonal lattice. Fejes Tóth (1940) proved that the hexagonal lattice isindeed the densest of all possible plane packings (Conway and Sloane 1993, pp. 8-9).

In 3-D, there are three periodic packings for identical spheres: cubic lattice, face-centered cubic lattice, and hexagonallattice. It was hypothesized by Kepler in 1611 that close packing (cubic or hexagonal) is the densest possible(has the greatest ), and this assertion is known as the Kepler Conjecture. The problem of finding the densestpacking of spheres (not necessarily periodic) is therefore known as the Kepler Problem. The Kepler Conjecture isintuitively obvious, but the proof remained elusive until it was accomplished in a series of papers by Hales culminating in1998. Gauß (1831) proved that the face-centered cubic is the densest lattice packing in 3-D (Conway andSloane 1993, p. 9). This result has since been extended to Hypersphere Packing.

In 3-D, face-centered cubic close packing and hexagonal close packing (which is distinct from hexagonal lattice), both give

(1)

(2)

``Random'' close packing in 3-D gives only (Jaeger and Nagel 1992).

The Packing Densities for several packing types are summarized in the following table.

Packing	(exact)	(approx.)
square lattice (2-D)		0.7854
hexagonal lattice (2-D)		0.9069
cubic lattice		0.5236
hexagonal lattice		0.6046
face-centered cubic lattice		0.7405
random	--	0.6400

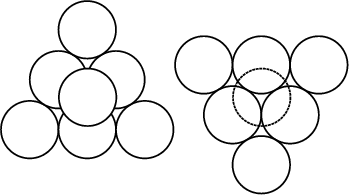
For cubic close packing, pack six Spheres together in the shape of an Equilateral Triangle and placeanother Sphere on top to create a Triangular Pyramid. Now create another such grouping of sevenSpheres and place the two Pyramids together facing in opposite directions. A Cubeemerges. Consider a face of the Cube, illustrated below.

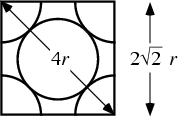
The ``unit cell'' cube contains eight -spheres (one at each Vertex) and sixHemispheres. The total Volume of Spheres in the unit cell is

			(3)

(4)

(5)

Hexagonal close packing must give the same values, since sliding one sheet of Spheres cannot affect thevolume they occupy. To verify this, construct a 3-D diagram containing a hexagonal unit cell with three layers. Both the topand the bottom contain six -Spheres and one Hemisphere. The total number of spheres in thesetwo rows is therefore

(6)

(7)

(8)

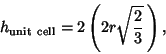(9)

(10)

If we had actually wanted to compute the Volume of Sphere inside and outside the HexagonalPrism, we could use the Spherical Cap equation to obtain

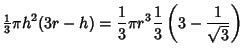			(11)
			(12)

The rigid packing with lowest density known has (Gardner 1966). To be Rigid, eachSphere must touch at least four others, and the four contact points cannot be in a single Hemisphere or all onone equator.

If spheres packed in a cubic lattice, face-centered cubic lattice, and hexagonal lattice are allowed to expand, they formcubes, hexagonal prisms, and rhombic dodecahedra. Compressing a random packing gives polyhedra with an average of 13.3faces (Coxeter 1958, 1961).

For sphere packing inside a Cube, see Goldberg (1971) and Schaer (1966).

Sphere Packings

Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed. New York: Springer-Verlag, 1993.

Coxeter, H. S. M. ``Close-Packing and so Forth.'' Illinois J. Math. 2, 746-758, 1958.

Coxeter, H. S. M. ``Close Packing of Equal Spheres.'' Section 22.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 405-411, 1961.

Coxeter, H. S. M. ``The Problem of Packing a Number of Equal Nonoverlapping Circles on a Sphere.'' Trans. New York Acad. Sci. 24, 320-331, 1962.

Critchlow, K. Order in Space: A Design Source Book. New York: Viking Press, 1970.

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 195-197, 1989.

Eppstein, D. ``Covering and Packing.''http://www.ics.uci.edu/~eppstein/junkyard/cover.html.

Fejes Tóth, G. ``Über einen geometrischen Satz.'' Math. Z. 46, 78-83, 1940.

Fejes Tóth, G. Lagerungen in der Ebene, auf der Kugel und in Raum, 2nd ed. Berlin: Springer-Verlag, 1972.

Gardner, M. ``Packing Spheres.'' Ch. 7 in Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, 1966.

Gauss, C. F. ``Besprechung des Buchs von L. A. Seeber: Intersuchungen über die Eigenschaften der positiven ternären quadratischen Formen usw.'' Göttingsche Gelehrte Anzeigen (1831, July 9) 2, 188-196, 1876.

Goldberg, M. ``On the Densest Packing of Equal Spheres in a Cube.'' Math. Mag. 44, 199-208, 1971.

Hales, T. C. ``The Sphere Packing Problem.'' J. Comput. Appl. Math 44, 41-76, 1992.

Jaeger, H. M. and Nagel, S. R. ``Physics of Granular States.'' Science 255, 1524, 1992.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 31, 1983.

Lindsey, J. H. II. ``Sphere Packing in .'' Math. 33, 137-147, 1986.

Muder, D. J. ``Putting the Best Face of a Voronoi Polyhedron.'' Proc. London Math. Soc. 56, 329-348, 1988.

Rogers, C. A. ``The Packing of Equal Spheres.'' Proc. London Math. Soc. 8, 609-620, 1958.

Rogers, C. A. Packing and Covering. Cambridge, England: Cambridge University Press, 1964.

Schaer, J. ``On the Densest Packing of Spheres in a Cube.'' Can. Math. Bul. 9, 265-270, 1966.

Sloane, N. J. A. ``The Packing of Spheres.'' Sci. Amer. 250, 116-125, 1984.

Stewart, I. The Problems of Mathematics, 2nd ed. Oxford, England: Oxford University Press, pp. 69-82, 1987.

Thompson, T. M. From Error-Correcting Codes Through Sphere Packings to Simple Groups. Washington, DC: Math. Assoc. Amer., 1984.

• Monge's Shuffle
• Monge's Theorem
• Monica Set
• Monic Polynomial
• Monkey and Coconut Problem
• Monkey Saddle
• Monochromatic Forced Triangle
• Monodromy
• Monodromy Group
• Monodromy Theorem
• Monogenic Function
• Monohedral Tiling
• Monoid
• Monomial
• Monomino
• Monomorph
• Monomorphism
• Monotone
• Monotone Decreasing
• Monotone Increasing
• Monotonic Function
• Monotonic Sequence
• Monotonic Voting
• Monster Group
• Monte Carlo Integration