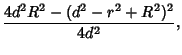| 释义 |
Sphere-Sphere IntersectionLet two spheres of Radii  and and 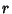 be located along the x-Axis centered at be located along the x-Axis centered at  and and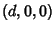 , respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.The equations of the two Spheres are , respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.The equations of the two Spheres are
Combining (1) and (2) gives
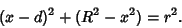 | (3) |
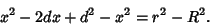 | (4) |
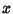 gives gives
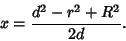 | (5) |
 -plane at asingle -plane at asingle 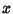 -coordinate. Plugging this back into (1) gives -coordinate. Plugging this back into (1) gives
which is a Circle with Radius
The Volume of the 3-D Lens common to the two spheres can be found by adding the two SphericalCaps. The distances from the Spheres' centers to the bases of the caps are
so the heights of the caps are
The Volume of a Spherical Cap of height 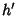 for a Sphere of Radius for a Sphere of Radius  is is
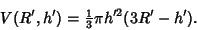 | (12) |
 and and  and summing the two caps gives and summing the two caps gives
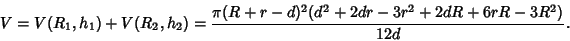 | (13) |
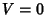 for for 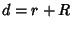 as it must. In the special case as it must. In the special case 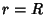 , the Volume simplifies to , the Volume simplifies to
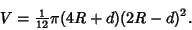 | (14) |
|

![]() and
and ![]() be located along the x-Axis centered at
be located along the x-Axis centered at ![]() and
and![]() , respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.The equations of the two Spheres are
, respectively. Not surprisingly, the analysis is very similar to the case of the Circle-Circle Intersection.The equations of the two Spheres are