“Carmichael Number”的概念、定义、习题解题方法及翻译-数学辞典

单词

Carmichael Number

释义

Carmichael Number

A Carmichael number is an Odd Composite Number which satisfies Fermat's Little Theorem

for every choice of

satisfying

(i.e.,

and

are Relatively Prime) with

. ACarmichael number is therefore a Pseudoprimes to any base. Carmichael numbers therefore cannot be found to beComposite using Fermat's Little Theorem. However, if

, the congruence ofFermat's Little Theorem is sometimes Nonzero, thus identifying a Carmichael number

asComposite.

Carmichael numbers are sometimes called Absolute Pseudoprimes and also satisfyKorselt's Criterion. R. D. Carmichael first noted the existence of such numbers in 1910, computed 15 examples, andconjectured that there were infinitely many (a fact finally proved by Alford et al. 1994).

The first few Carmichael numbers are 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, ... (Sloane's A002997). Carmichael numbers have at least three Prime Factors. For Carmichael numbers with exactly threePrime Factors, once one of the Primes has been specified, there are only a finite number ofCarmichael numbers which can be constructed. Numbers of the form are Carmichael numbers ifeach of the factors is Prime (Korselt 1899, Ore 1988, Guy 1994). This can be seen since for

is a multiple of

and the Least Common Multiple of

, and

, so

modulo each of the Primes

, and

, hence

modulo their product.The first few such Carmichael numbers correspond to

, 6, 35, 45, 51, 55, 56, ... (Sloane's A046025) and are 1729, 294409,56052361, 118901521, ... (Sloane's A033502). The largest known Carmichael number of this form was found by H. Dubner in 1996and has 1025 digits.

The smallest Carmichael numbers having 3, 4, ... factors are , , 825265, 321197185, ... (Sloane's A006931). In total, there are only 43Carmichael numbers , 2163 , 105,212 , and 246,683 (Pinch 1993).Let denote the number of Carmichael numbers less than . Then, for sufficiently large ( fromnumerical evidence),

(Alford et al. 1994).

The Carmichael numbers have the following properties:

: 1. If a Prime divides the Carmichael number 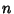, then implies that .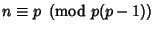
: 2. Every Carmichael number is Squarefree.
: 3. An Odd Composite Squarefree number 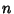is a Carmichael number Iff 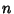divides theDenominator of the Bernoulli Number .

See also Carmichael Condition, Pseudoprime

References

Alford, W. R.; Granville, A.; and Pomerance, C. ``There are Infinitely Many Carmichael Numbers.'' Ann. Math. 139, 703-722, 1994.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 87, 1987.

Guy, R. K. ``Carmichael Numbers.'' §A13 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 30-32, 1994.

Korselt, A. ``Problème chinois.'' L'intermédiaire math. 6, 143-143, 1899.

Ore, Ø. Number Theory and Its History. New York: Dover, 1988.

Pinch, R. G. E. ``The Carmichael Numbers up to .'' Math. Comput. 55, 381-391, 1993.

Pinch, R. G. E. ftp://emu.pmms.cam.ac.uk/pub/Carmichael/.

Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. ``The Pseudoprimes to .'' Math. Comput. 35, 1003-1026, 1980.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Basel: Birkhäuser, pp. 89-90 and 94-95, 1994.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 116, 1993.

Sloane, N. J. A. Sequences A002997/M5462, A006931/M5463, A033502, and A046025 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。