Steenrod Algebra

The Steenrod algebra has to do with the Cohomology operations in singular Cohomology with Integer mod2 Coefficients. For every and there are naturaltransformations of Functors

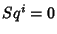1. for .

2. 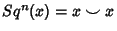for all and all pairs .

3. .

4. The maps commute with the coboundary maps in the long exact sequence of a pair. In other words,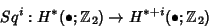

is a degree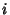 transformation of cohomology theories.

5. (Cartan Relation)

6. (Adem Relations) For ,

7. where is the cohomology suspension isomorphism.

The existence of these cohomology operations endows the cohomology ring with the structure of a Module over theSteenrod algebra , defined to be , where is the free module functor that takes any set and sends it to the free module overthat set. We think of as being a graded module, where the-th gradation is given by . This makes the tensor algebra into a Graded Algebra over . is the Ideal generated by the elements and for . This makes into a graded algebra.

By the definition of the Steenrod algebra, for any Space , is a Module over theSteenrod algebra , with multiplication induced by . With the above definitions,cohomology with Coefficients in the Ring , is a Functorfrom the category of pairs of Topological Spaces to graded modules over .

• Positive Semidefinite Matrix
• Positive Semidefinite Quadratic Form
• Postage Stamp Problem
• Posterior Distribution
• Postnikov System
• Postulate
• Potato Paradox
• Potential Function
• Potential Theory
• Pothenot Problem
• Poulet Number
• Power
• Power Center
• Power (Circle)
• Power Curve
• Powerfree
• Powerful Number
• Power Line
• Power Point
• Power Rule
• Power Series
• Power Set
• Power Spectrum
• Power (Statistics)
• Power Tower