| 释义 |
Chebyshev Differential Equation
 | (1) |
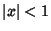 . The Chebyshev differential equation has regular Singularities at . The Chebyshev differential equation has regular Singularities at  , 1, and , 1, and 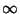 . It can be solved by series solution using the expansions . It can be solved by series solution using the expansions
Now, plug (2-4) into the original equation (1) to obtain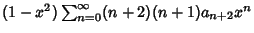 | | 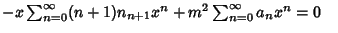 | (5) |
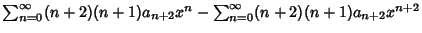 | | 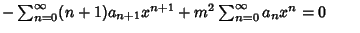 | (6) |
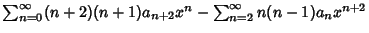 | | 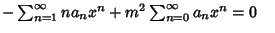 | (7) |
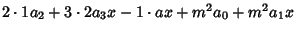 | | 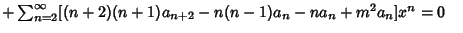 | (8) |
 | | 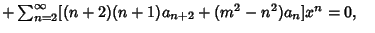 | (9) |
so
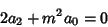 | (10) |
 | (11) |
 | (12) |
 | (13) |
and for the Odd Coefficients
So the general solution is | | 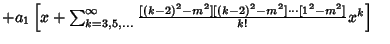 | (20) |
If 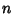 is Even, then is Even, then 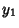 terminates and is a Polynomial solution, whereas if terminates and is a Polynomial solution, whereas if 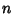 is Odd, then is Odd, then  terminates and isa Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the FirstKind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation terminates and isa Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the FirstKind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation
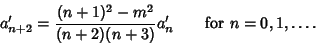 | (21) |
|
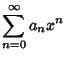
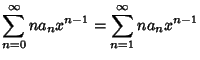
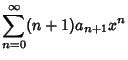
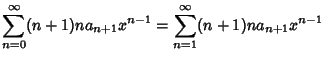
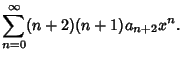



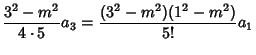
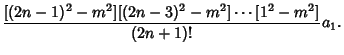
![]() is Even, then
is Even, then ![]() terminates and is a Polynomial solution, whereas if
terminates and is a Polynomial solution, whereas if ![]() is Odd, then
is Odd, then ![]() terminates and isa Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the FirstKind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation
terminates and isa Polynomial solution. The Polynomial solutions defined here are known as Chebyshev Polynomials of the FirstKind. The definition of the Chebyshev Polynomial of the Second Kind gives a similar, but distinct, recurrence relation