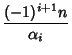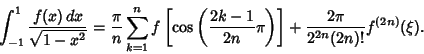| 释义 |
Chebyshev-Gauss QuadratureAlso called Chebyshev Quadrature. A Gaussian Quadrature over the interval 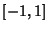 with Weighting Function with Weighting Function . The Abscissas for quadrature order . The Abscissas for quadrature order 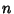 are given by the roots of theChebyshev Polynomial of the First Kind are given by the roots of theChebyshev Polynomial of the First Kind 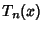 , which occursymmetrically about 0. The Weights are , which occursymmetrically about 0. The Weights are
 | (1) |
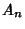 is the Coefficient of is the Coefficient of  in in 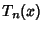 . For Hermite Polynomials, . For Hermite Polynomials,
 | (2) |
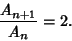 | (3) |
 | (4) |
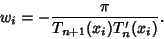 | (5) |
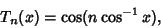 | (6) |
 | (7) |
where
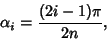 | (10) |
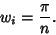 | (11) |
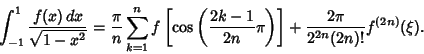 | (12) |
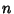 |  |  | | 2 | ± 0.707107 | 1.5708 | | 3 | 0 | 1.0472 | | | ± 0.866025 | 1.0472 | | 4 | ± 0.382683 | 0.785398 | | | ± 0.92388 | 0.785398 | | 5 | 0 | 0.628319 | | | ± 0.587785 | 0.628319 | | | ± 0.951057 | 0.628319 |
ReferencesHildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 330-331, 1956.
|
![]() with Weighting Function
with Weighting Function![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() are given by the roots of theChebyshev Polynomial of the First Kind
are given by the roots of theChebyshev Polynomial of the First Kind ![]() , which occursymmetrically about 0. The Weights are
, which occursymmetrically about 0. The Weights are