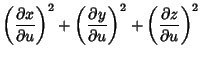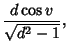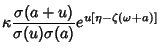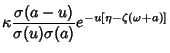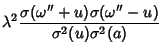| 释义 |
Oblate Spheroid GeodesicThe Geodesic on an Oblate Spheroid can be computed analytically for a spheroid specified parametricallyby
with 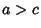 , although it is much more unwieldy than for a simple Sphere. Using the first Partial Derivatives , although it is much more unwieldy than for a simple Sphere. Using the first Partial Derivatives
 | (4) |
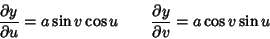 | (5) |
 | (6) |
 | (7) |
 | (8) |
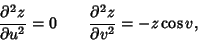 | (9) |
Since  and and  and and 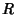 are explicit functions of are explicit functions of 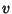 only, we can use the special form of the Geodesicequation. only, we can use the special form of the Geodesicequation.
Integrating gives
 | (14) |
 is an Elliptic Integral of the First Kind with Parameter is an Elliptic Integral of the First Kind with Parameter  , and , and  isan Elliptic Integral of the Third Kind. isan Elliptic Integral of the Third Kind.
Geodesics other than Meridians of an Oblate Spheroid undulate between twoparallels with latitudes equidistant from the equator. Using the Weierstraß Sigma Function and Weierstraß Zeta Function, the Geodesic on the OblateSpheroid can be written as
(Forsyth 1960, pp. 108-109; Halphen 1886-1891).
The equation of the Geodesic can be put in the form
 | (20) |
 is the smallest value of is the smallest value of 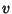 on the curve. Furthermore, the difference in longitude between points ofhighest and next lowest latitude on the curve is on the curve. Furthermore, the difference in longitude between points ofhighest and next lowest latitude on the curve is
 | (21) |
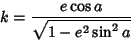 | (22) |
References
Forsyth, A. R. Calculus of Variations. New York: Dover, 1960.Halphen, G. H. Traité des fonctions elliptiques et de leurs applications fonctions elliptiques, Vol. 2. Paris: Gauthier-Villars, pp. 238-243, 1886-1891.
|