“Obtuse Triangle”的概念、定义、习题解题方法及翻译-数学辞典

单词

Obtuse Triangle

释义

Obtuse Triangle

An obtuse triangle is a Triangle in which one of the Angles is an Obtuse Angle. (Obviously, only a single Angle in a Triangle can be Obtuse or it wouldn't be aTriangle.) A triangle must be either obtuse, Acute, or Right.

A famous problem is to find the chance that three points picked randomly in a Plane are the Vertices of an obtuse triangle (Eisenberg and Sullivan 1996). Unfortunately, the solution of the problem depends on theprocedure used to pick the ``random'' points (Portnoy 1994). In fact, it is impossible to pick random variables which areuniformly distributed in the plane (Eisenberg and Sullivan 1996). Guy (1993) gives a variety of solutions to the problem. Woolhouse (1886) solved the problem by picking uniformly distributed points in the unit Disk, and obtained

(1)

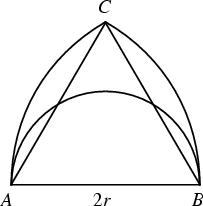
The problem was generalized by Hall (1982) to

-D Ball Triangle Picking, and Buchta (1986) gave closed form evaluations for Hall's integrals.

Lewis Carroll (1893) posed and gave another solution to the problem as follows. Call the longest side of a Triangle, and call the Diameter . Draw arcs from and of Radius . Because the longest side of theTriangle is defined to be , the third Vertex of the Triangle must lie withinthe region . If the third Vertex lies within the Semicircle, the Triangle isan obtuse triangle. If the Vertex lies on the Semicircle (which will happen withprobability 0), the Triangle is a Right Triangle. Otherwise, it is an Acute Triangle. The chance ofobtaining an obtuse triangle is then the ratio of the Area of the Semicircle to that of . TheArea of is then twice the Area of a Sector minus the Area of the Triangle.

(2)

Therefore,

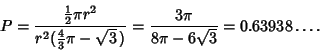(3)

Let the Vertices of a triangle in -D be Normal(Gaussian) variates. The probability that a Gaussian triangle in -D is obtuse is



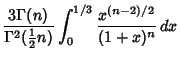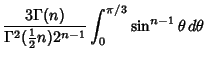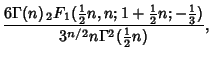			(4)

where

is the Gamma Function and

is theHypergeometric Function. For Even

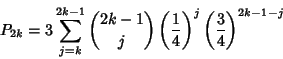(5)

(Eisenberg and Sullivan 1996). The first few cases are explicitly

			(6)
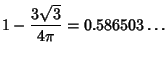			(7)
			(8)
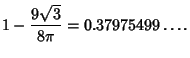			(9)

See also Acute Angle, Acute Triangle, Ball Triangle Picking,Obtuse Angle, Right Triangle, Triangle

References

Buchta, C. ``A Note on the Volume of a Random Polytope in a Tetrahedron.'' Ill. J. Math. 30, 653-659, 1986.

Carroll, L. Pillow Problems & A Tangled Tale. New York: Dover, 1976.

Eisenberg, B. and Sullivan, R. ``Random Triangles Dimensions.'' Amer. Math. Monthly 103, 308-318, 1996.

Guy, R. K. ``There are Three Times as Many Obtuse-Angled Triangles as There are Acute-Angled Ones.'' Math. Mag. 66, 175-178, 1993.

Hall, G. R. ``Acute Triangles in the -Ball.'' J. Appl. Prob. 19, 712-715, 1982.

Portnoy, S. ``A Lewis Carroll Pillow Problem: Probability on at Obtuse Triangle.'' Statist. Sci. 9, 279-284, 1994.

Wells, D. G. The Penguin Book of Interesting Puzzles. London: Penguin Books, pp. 67 and 248-249, 1992.

Woolhouse, W. S. B. Solution to Problem 1350. Mathematical Questions, with Their Solutions, from the Educational Times, 1. London: F. Hodgson and Son, 49-51, 1886.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。