“Tetrahedral Number”的概念、定义、习题解题方法及翻译-数学辞典

单词

Tetrahedral Number

释义

Tetrahedral Number

A Figurate Number of the form

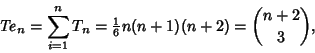(1)

where

is the

th Triangular Number and

is a Binomial Coefficient. These numberscorrespond to placing discrete points in the configuration of a Tetrahedron (triangular base pyramid). Tetrahedralnumbers are Pyramidal Numbers with

, and are the sum of consecutive TriangularNumbers. The first few are 1, 4, 10, 20, 35, 56, 84, 120, ... (Sloane's A000292). The GeneratingFunction of the tetrahedral numbers is

(2)

Tetrahedral numbers are Even, except for every fourth tetrahedral number, which is Odd (Conway and Guy 1996).

The only numbers which are simultaneously Square and Tetrahedral are, , and (giving , , and ), as proved by Meyl(1878; cited in Dickson 1952, p. 25). Numbers which are simultaneously Triangular andtetrahedral satisfy the Binomial Coefficient equation

(3)

and are given by

, and

(Guy 1994, p. 147). Beukers (1988) has studied the problem of finding numbers which are simultaneously tetrahedral andPyramidal via Integer points on an Elliptic Curve, and finds that the only solutionis the trivial

See also Pyramidal Number, Truncated Tetrahedral Number

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.

Beukers, F. ``On Oranges and Integral Points on Certain Plane Cubic Curves.'' Nieuw Arch. Wisk. 6, 203-210, 1988.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 44-46, 1996.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, 1952.

Guy, R. K. ``Figurate Numbers.'' §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 147-150, 1994.

Meyl, A.-J.-J. ``Solution de Question 1194.'' Nouv. Ann. Math. 17, 464-467, 1878.

Sloane, N. J. A. SequenceA000292/M3382in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。