| 释义 |
One-Ninth ConstantN.B. A detailed on-line essay by S. Finchwas the starting point for this entry.
Let  be Chebyshev Constants. Schönhage (1973) proved that be Chebyshev Constants. Schönhage (1973) proved that
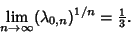 | (1) |
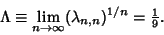 | (2) |
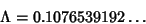 | (3) |
 is given by is given by
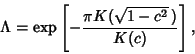 | (4) |
 is the complete Elliptic Integral of the First Kind, and is the complete Elliptic Integral of the First Kind, and  is the Parameter which solves is the Parameter which solves
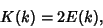 | (5) |
 is the complete Elliptic Integral of the Second Kind. This gives the value for is the complete Elliptic Integral of the Second Kind. This gives the value for  computed by Carpenter et al. (1984) computed by Carpenter et al. (1984)  is also given by the unique Positive Root of is also given by the unique Positive Root of
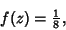 | (6) |
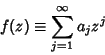 | (7) |
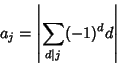 | (8) |
 may also be computed by writing may also be computed by writing 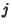 as as
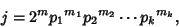 | (9) |
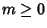 and and  , then , then
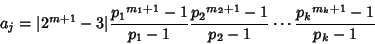 | (10) |
 is due to Magnus (1986). is due to Magnus (1986).  is the unique solutionwith is the unique solutionwith  of of
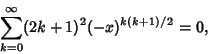 | (11) |
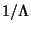 is sometimes calledVarga's Constant.See also Chebyshev Constants, Halphen Constant, Varga's Constant is sometimes calledVarga's Constant.See also Chebyshev Constants, Halphen Constant, Varga's Constant
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/onenin/onenin.htmlCarpenter, A. J.; Ruttan, A.; and Varga, R. S. ``Extended Numerical Computations on the ` ' Conjecture in Rational Approximation Theory.'' In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga). New York: Springer-Verlag, pp. 383-411, 1984. ' Conjecture in Rational Approximation Theory.'' In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga). New York: Springer-Verlag, pp. 383-411, 1984. Cody, W. J.; Meinardus, G.; and Varga, R. S. ``Chebyshev Rational Approximations to 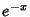 in in  and Applications to Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969. and Applications to Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969. Dunham, C. B. and Taylor, G. D. ``Continuity of Best Reciprocal Polynomial Approximation on 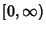 .'' J. Approx. Th. 30, 71-79, 1980. .'' J. Approx. Th. 30, 71-79, 1980. Gonchar, A. A. ``Rational Approximations of Analytic Functions.'' Amer. Math. Soc. Transl. Ser. 2 147, 25-34, 1990. Gonchar, A. A. and Rakhmanov, E. A. ``Equilibrium Distributions and Degree of Rational Approximation of Analytic Functions.'' Math. USSR Sbornik 62, 305-348, 1980. Magnus, A. P. ``On Freud's Equations for Exponential Weights, Papers Dedicated to the Memory of Géza Freud.'' J. Approx. Th. 46, 65-99, 1986. Rahman, Q. I. and Schmeisser, G. ``Rational Approximation to the Exponential Function.'' In Padé and Rational Approximation, (Proc. Internat. Sympos., Univ. South Florida, Tampa, Fla., 1976) (Ed. E. B. Saff and R. S. Varga). New York: Academic Press, pp. 189-194, 1977. Schönhage, A. ``Zur rationalen Approximierbarkeit von 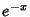 über über 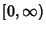 .'' J. Approx. Th. 7, 395-398, 1973. .'' J. Approx. Th. 7, 395-398, 1973. Varga, R. S. Scientific Computations on Mathematical Problems and Conjectures. Philadelphia, PA: SIAM, 1990.
|
![]() be Chebyshev Constants. Schönhage (1973) proved that
be Chebyshev Constants. Schönhage (1973) proved that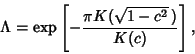
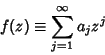
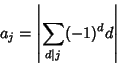
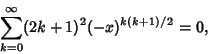
![]() ' Conjecture in Rational Approximation Theory.'' In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga). New York: Springer-Verlag, pp. 383-411, 1984.
' Conjecture in Rational Approximation Theory.'' In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga). New York: Springer-Verlag, pp. 383-411, 1984.![]() in
in ![]() and Applications to Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.
and Applications to Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.![]() .'' J. Approx. Th. 30, 71-79, 1980.
.'' J. Approx. Th. 30, 71-79, 1980.![]() über
über ![]() .'' J. Approx. Th. 7, 395-398, 1973.
.'' J. Approx. Th. 7, 395-398, 1973.