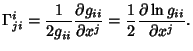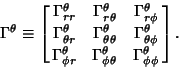| 释义 |
Connection CoefficientA quantity also known as a Christoffel Symbol of the Second Kind. Connection Coefficients are defined by
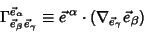 | (1) |
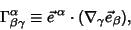 | (2) |
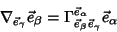 | (3) |
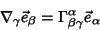 | (4) |
Connection Coefficients are not Tensors, but have Tensor-like Contravariant and Covariant indices. A fully Covariantconnection Coefficient is given by
 | (5) |
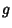 s are the Metric Tensors, the s are the Metric Tensors, the 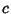 s are Commutation Coefficients, and the commas indicate the Comma Derivative. In an Orthonormal Basis, s are Commutation Coefficients, and the commas indicate the Comma Derivative. In an Orthonormal Basis, 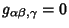 and and  , so , so
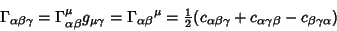 | (6) |
For Tensors of Rank 3, the connection Coefficients may beconcisely summarized in Matrix form:
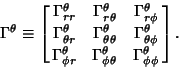 | (13) |
Connection Coefficients arise in the computation of Geodesics. The GeodesicEquation of free motion is
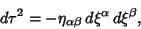 | (14) |
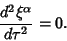 | (15) |
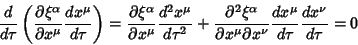 | (16) |
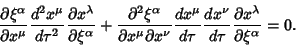 | (17) |
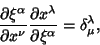 | (18) |
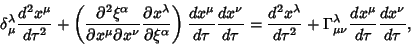 | (19) |
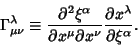 | (20) |
|