Consecutive Number Sequences
Consecutive number sequences are sequences constructed by concatenating numbers of a given type. Many of these sequences wereconsidered by Smarandache, so they are sometimes known as Smarandache Sequences.
The ![]() th term of the consecutive integer sequence consists of the concatenation of the first
th term of the consecutive integer sequence consists of the concatenation of the first ![]() Positive integers: 1,12, 123, 1234, ... (Sloane's A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998). Thissequence gives the digits of the Champernowne Constant and contains no Primes in the first 5,742 terms (Weisstein).This is roughly consistent with simple arguments based on the distribution of primes which suggest that only a single primeis expected in the first 15,000 or so terms. The number of digits of the
Positive integers: 1,12, 123, 1234, ... (Sloane's A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998). Thissequence gives the digits of the Champernowne Constant and contains no Primes in the first 5,742 terms (Weisstein).This is roughly consistent with simple arguments based on the distribution of primes which suggest that only a single primeis expected in the first 15,000 or so terms. The number of digits of the ![]() term can be computed by noticing the pattern in the following table, where
term can be computed by noticing the pattern in the following table, where ![]() is the number of digits in
is the number of digits in ![]() .
.
| Digits | ||
| 1 | 1-9 | |
| 2 | 10-99 | |
| 3 | 100-999 | |
| 4 | 1000-9999 |
Therefore, the number of digits ![]() in the
in the ![]() th term can be written
th term can be written
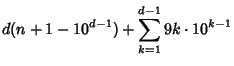 | |||
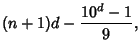 |
where the second term is the Repunit
The ![]() th term of the reverse integer sequence consists of the concatenation of the first
th term of the reverse integer sequence consists of the concatenation of the first ![]() Positive integers writtenbackwards: 1, 21, 321, 4321, ... (Sloane's A000422; Smarandache 1993, Dumitrescu and Seleacu 1994, Stephan 1998). The onlyPrime in the first 4,707 terms (Weisstein) of this sequence is the 82nd term 828180...321 (Stephan 1998), which has 155 digits.This is roughly consistent with simple arguments based on the distribution of prime which suggest that a single primeis expected in the first 15,000 or so terms. The terms of the reverse integer sequence have the same number of digitsas do the consecutive integer sequence.
Positive integers writtenbackwards: 1, 21, 321, 4321, ... (Sloane's A000422; Smarandache 1993, Dumitrescu and Seleacu 1994, Stephan 1998). The onlyPrime in the first 4,707 terms (Weisstein) of this sequence is the 82nd term 828180...321 (Stephan 1998), which has 155 digits.This is roughly consistent with simple arguments based on the distribution of prime which suggest that a single primeis expected in the first 15,000 or so terms. The terms of the reverse integer sequence have the same number of digitsas do the consecutive integer sequence.
The concatenation of the first ![]() A019518; Smith 1996, Mudge 1997). Thissequence converges to the digits of the Copeland-Erdös Constant and is Prime forterms 1, 2, 4, 128, 174, 342, 435, 1429, ... (Sloane's A046035; Ibstedt 1998, pp. 78-79), with no others less than 3,219 (Weisstein).
A019518; Smith 1996, Mudge 1997). Thissequence converges to the digits of the Copeland-Erdös Constant and is Prime forterms 1, 2, 4, 128, 174, 342, 435, 1429, ... (Sloane's A046035; Ibstedt 1998, pp. 78-79), with no others less than 3,219 (Weisstein).
The concatenation of the first ![]() A019519;Smith 1996, Marimutha 1997, Mudge 1997). This sequence is Prime for terms 2, 10, 16, 34, 49, 2570, ...(Sloane's A046036; Weisstein, Ibstedt 1998, pp. 75-76), with no others less than 3,405 (Weisstein). The 2570th term, given by 13 5 7...5137 5139, has 9725 digits and was discovered by Weisstein in Aug. 1998.
A019519;Smith 1996, Marimutha 1997, Mudge 1997). This sequence is Prime for terms 2, 10, 16, 34, 49, 2570, ...(Sloane's A046036; Weisstein, Ibstedt 1998, pp. 75-76), with no others less than 3,405 (Weisstein). The 2570th term, given by 13 5 7...5137 5139, has 9725 digits and was discovered by Weisstein in Aug. 1998.
The concatenation of the first ![]() A019520;Smith 1996; Marimutha 1997; Mudge 1997; Ibstedt 1998, pp. 77-78).
A019520;Smith 1996; Marimutha 1997; Mudge 1997; Ibstedt 1998, pp. 77-78).
The concatenation of the first ![]() A019521;Marimutha 1997). The only Prime in the first 2,786 terms is the third term, 149, (Weisstein).
A019521;Marimutha 1997). The only Prime in the first 2,786 terms is the third term, 149, (Weisstein).
The concatenation of the first ![]() A019522;Marimutha 1997). There are no Primes in the first 2,652 terms (Weisstein).
A019522;Marimutha 1997). There are no Primes in the first 2,652 terms (Weisstein).
References
Dumitrescu, C. and Seleacu, V. (Ed.). Some Notions and Questions in Number Theory. Glendale, AZ: Erhus University Press, 1994. Ibstedt, H. ``Smarandache Concatenated Sequences.'' Ch. 5 in Computer Analysis of Number Sequences. Lupton, AZ: American Research Press, pp. 75-79, 1998. Marimutha, H. ``Smarandache Concatenate Type Sequences.'' Bull. Pure Appl. Sci. 16E, 225-226, 1997. Mudge, M. ``Top of the Class.'' Personal Computer World, 674-675, June 1995. Mudge, M. ``Not Numerology but Numeralogy!'' Personal Computer World, 279-280, 1997. Sloane, N. J. A. Sequences A000422, A007908, A019518, A019519, A019520, A019521, A019522, A046035, and A046036 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993. Smith, S. ``A Set of Conjectures on Smarandache Sequences.'' Bull. Pure Appl. Sci. 15E, 101-107, 1996. Stephan, R. W. ``Factors and Primes in Two Smarandache Sequences.'' Smarandache Notions J. 9, 4-10, 1998. http://www.tmt.de/~stephan/sm.dvi.gz.
- Kimberling Sequence
- Kimberling Shuffle
- Kings Problem
- King Walk
- Kinney's Set
- Kinoshita-Terasaka Knot
- Kinoshita-Terasaka Mutants
- Kirby Calculus
- Kirby's List
- Kirkman's Schoolgirl Problem
- Kirkman Triple System
- Kissing Circles Problem
- Kissing Number
- Kiss Surface
- Kite
- Klarner-Rado Sequence
- Klarner's Theorem
- Klein-Beltrami Model
- Klein Bottle
- Klein Four-Group
- Klein-Gordon Equation
- Kleinian Group
- Klein Quartic
- Klein's Absolute Invariant
- Klein's Equation