Thurston's Geometrization Conjecture
Thurston's conjecture has to do with geometric structures on 3-D Manifolds. Before stating Thurston'sconjecture, some background information is useful. 3-dimensional Manifolds possess what is known as astandard 2-level Decomposition. First, there is the Connected Sum Decomposition, which says that everyCompact 3-Manifold is the Connected Sum of a unique collection ofPrime 3-Manifolds.
The second Decomposition is the Jaco-Shalen-Johannson Torus Decomposition, which states that irreducibleorientable Compact 3-Manifolds have a canonical (up to Isotopy)minimal collection of disjointly Embedded incompressible Tori such that eachcomponent of the 3-Manifold removed by the Tori is either ``atoroidal'' or ``Seifert-fibered.''
Thurston's conjecture is that, after you split a 3-Manifold into its Connected Sum and then Jaco-Shalen-Johannson Torus Decomposition, the remaining components each admit exactly oneof the following geometries:
- 1. Euclidean Geometry,
- 2. Hyperbolic Geometry,
- 3. Spherical Geometry,
- 4. the Geometry of
, - 5. the Geometry of
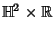, - 6. the Geometry of
, - 7. Nil Geometry, or
- 8. Sol Geometry.
is the 2-Sphere and 
is the Hyperbolic Plane. If Thurston's conjecture istrue, the truth of the Poincaré Conjecture immediately follows.See also Connected Sum Decomposition, Euclidean Geometry, Hyperbolic Geometry,Jaco-Shalen-Johannson Torus Decomposition, Nil Geometry, Poincaré Conjecture, Sol Geometry, Spherical Geometry- Sampling Theorem
- Sandwich Theorem
- San Marco Fractal
- Sard's Theorem
- Sarkovskii's Theorem
- Sarrus Linkage
- Sarrus Number
- SAS Theorem
- Satellite Knot
- Satisfiability Problem
- Sausage Conjecture
- Savitzky-Golay Filter
- Savoy Knot
- Scalar
- Scalar Curvature
- Scalar Field
- Scalar Function
- Scalar Potential
- Scalar Triple Product
- Scale
- Scale Factor
- Scalene Triangle
- Scaling
- Scattering Operator
- Scattering Theory