“Topology”的概念、定义、习题解题方法及翻译-数学辞典

单词

Topology

释义

Topology

Topology is the mathematical study of properties of objects which are preserved through deformations, twistings, andstretchings. (Tearing, however, is not allowed.) A Circle is topologically equivalent to an Ellipse (intowhich it can be deformed by stretching) and a Sphere is equivalent to an Ellipsoid. Continuing along theselines, the Space of all positions of the minute hand on a clock is topologically equivalent to a Circle(where Space of all positions means ``the collection of all positions''). Similarly, the Space of allpositions of the minute and hour hands is equivalent to a Torus. The Space of all positions of the hour,minute and second hands form a 4-D object that cannot be visualized quite as simply as the former objects since it cannotbe placed in our 3-D world, although it can be visualized by other means.

There is more to topology, though. Topology began with the study of curves, surfaces, and other objects in the plane and3-space. One of the central ideas in topology is that spatial objects like Circles andSpheres can be treated as objects in their own right, and knowledge of objects is independent of howthey are ``represented'' or ``embedded'' in space. For example, the statement ``if you remove a point from aCircle, you get a line segment'' applies just as well to the Circle as to an Ellipse, and even totangled or knotted Circles, since the statement involves only topological properties.

Topology has to do with the study of spatial objects such as curves, surfaces, the space we call our universe, thespace-time of general relativity, fractals, knots, manifolds (objects with some of the same basic spatial properties as ouruniverse), phase spaces that are encountered in physics (such as the space of hand-positions of a clock), symmetrygroups like the collection of ways of rotating a top, etc.

The ``objects'' of topology are often formallydefined as Topological Spaces. If two objects have the same topological properties, they aresaid to be Homeomorphic (although, strictly speaking, properties that are not destroyed by stretching and distortingan object are really properties preserved by Isotopy, not Homeomorphism; Isotopy has to do withdistorting embedded objects, while Homeomorphism is intrinsic).

Topology is divided into Algebraic Topology (also called Combinatorial Topology), DifferentialTopology, and Low-Dimensional Topology.

There is also a formal definition for a topology defined in terms of set operations. A Set along with acollection of Subsets of it is said to be a topology if the Subsets in obeythe following properties:

: 1. The (trivial) subsets and the Empty Set are in .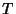
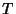: 2. Whenever sets and are in , then so is .
: 3. Whenever two or more sets are in 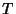, then so is their Union

(Bishop and Goldberg 1980).

A Set for which a topology has been specified is called a Topological Space (Munkres 1975, p. 76).For example, the Set together with the Subsets, , , comprises a topology, and is a Topological Space.

Topologies can be built up from Topological Bases. For the Real Numbers, the topology is the Union of Open Intervals.

See also Algebraic Topology, Differential Topology, Genus, Klein Bottle,Kuratowski Reduction Theorem, Lefshetz Trace Formula, Low-Dimensional Topology, Point-SetTopology, Zariski Topology

References

Topology

Adamson, I. A General Topology Workbook. Boston, MA: Birkhäuser, 1996.

Armstrong, M. A. Basic Topology, rev. New York: Springer-Verlag, 1997.

Barr, S. Experiments in Topology. New York: Dover, 1964.

Berge, C. Topological Spaces Including a Treatment of Multi-Valued Functions, Vector Spaces and Convexity. New York: Dover, 1997.

Bishop, R. and Goldberg, S. Tensor Analysis on Manifolds. New York: Dover, 1980.

Blackett, D. W. Elementary Topology: A Combinatorial and Algebraic Approach. New York: Academic Press, 1967.

Bloch, E. A First Course in Geometric Topology and Differential Geometry. Boston, MA: Birkhäuser, 1996.

Chinn, W. G. and Steenrod, N. E. First Concepts of Topology: The Geometry of Mappings of Segments, Curves, Circles, and Disks. Washington, DC: Math. Assoc. Amer., 1966.

Eppstein, D. ``Geometric Topology.''http://www.ics.uci.edu/~eppstein/junkyard/topo.html.

Francis, G. K. A Topological Picturebook. New York: Springer-Verlag, 1987.

Gemignani, M. C. Elementary Topology. New York: Dover, 1990.

Greever, J. Theory and Examples of Point-Set Topology. Belmont, CA: Brooks/Cole, 1967.

Hirsch, M. W. Differential Topology. New York: Springer-Verlag, 1988.

Hocking, J. G. and Young, G. S. Topology. New York: Dover, 1988.

Kahn, D. W. Topology: An Introduction to the Point-Set and Algebraic Areas. New York: Dover, 1995.

Kelley, J. L. General Topology. New York: Springer-Verlag, 1975.

Kinsey, L. C. Topology of Surfaces. New York: Springer-Verlag, 1993.

Lipschutz, S. Theory and Problems of General Topology. New York: Schaum, 1965.

Mendelson, B. Introduction to Topology. New York: Dover, 1990.

Munkres, J. R. Elementary Differential Topology. Princeton, NJ: Princeton University Press, 1963.

Munkres, J. R. Topology: A First Course. Englewood Cliffs, NJ: Prentice-Hall, 1975.

Praslov, V. V. and Sossinsky, A. B. Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology. Providence, RI: Amer. Math. Soc., 1996.

Shakhmatv, D. and Watson, S. ``Topology Atlas.'' http://www.unipissing.ca/topology/.

Steen, L. A. and Seebach, J. A. Jr. Counterexamples in Topology. New York: Dover, 1996.

Thurston, W. P. Three-Dimensional Geometry and Topology, Vol. 1. Princeton, NJ: Princeton University Press, 1997.

van Mill, J. and Reed, G. M. (Eds.). Open Problems in Topology. New York: Elsevier, 1990.

Veblen, O. Analysis Situs, 2nd ed. New York: Amer. Math. Soc., 1946.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。