Towers of Hanoi
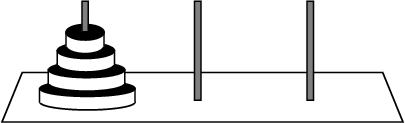
A Puzzle invented by E. Lucas in 1883. Given a stack of 
disks arranged from largest on the bottom to smallest ontop placed on a rod, together with two empty rods, the towers of Hanoi puzzle asks for the minimum number of moves requiredto reverse the order of the stack (where moves are allowed only if they place smaller disks on top of larger disks). Theproblem is Isomorphic to finding a Hamiltonian Path on an -Hypercube.
For disks, the number of moves 
required is given by the Recurrence Relation
Solving gives
The number of disks moved after the
th step is the same as the element which needs to be added or deleted in theth Addend of the Ryser Formula (Gardner 1988, Vardi 1991).A Hanoi Graph can be constructed whose Vertices correspond to legal configurations of towers of Hanoi, where the Vertices are adjacent if the corresponding configurations can beobtained by a legal move. It can be solved using a binary Gray Code.
Poole (1994) gives Mathematica
(Wolfram Research, Champaign, IL) routines for solving an arbitrary diskconfiguration in the fewest possible moves. The proof of minimality is achieved using the Lucas Correspondencewhich relates Pascal's Triangle to the Hanoi Graph. Algorithms are known fortransferring disks for four pegs, but none has been proved minimal. For additional references, see Poole (1994).
References
Bogomolny, A. ``Towers of Hanoi.'' http://www.cut-the-knot.com/recurrence/hanoi.html. Chartrand, G. ``The Tower of Hanoi Puzzle.'' §6.3 in Introductory Graph Theory. New York: Dover, pp. 135-139, 1985. Dubrovsky, V. ``Nesting Puzzles, Part I: Moving Oriental Towers.'' Quantum 6, 53-57 (Jan.) and 49-51 (Feb.), 1996. Gardner, M. ``The Icosian Game and the Tower of Hanoi.'' Ch. 6 in The Scientific American Book of Mathematical Puzzles & Diversions. New York: Simon and Schuster, 1959. Kasner, E. and Newman, J. R. Mathematics and the Imagination. Redmond, WA: Tempus Books, pp. 169-171, 1989. Kolar, M. ``Towers of Hanoi.'' http://www.pangea.ca/kolar/javascript/Hanoi/Hanoi.html. Poole, D. G. ``The Towers and Triangles of Professor Claus (or, Pascal Knows Hanoi).'' Math. Mag. 67, 323-344, 1994. Ruskey, F. ``Towers of Hanoi.'' http://sue.csc.uvic.ca/~cos/inf/comb/SubsetInfo.html#Hanoi. Schoutte, P. H. ``De Ringen van Brahma.'' Eigen Haard 22, 274-276, 1884. Kraitchik, M. ``The Tower of Hanoi.'' §3.12.4 in Mathematical Recreations. New York: W. W. Norton, pp. 91-93, 1942. Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 111-112, 1991.
Poole, D. G. ``Towers of Hanoi.'' http://www.astro.virginia.edu/~eww6n/math/notebooks/Hanoi.m.
- Spinode
- Spinor
- Spiral
- Spiral Point
- Spira Mirabilis
- Spiric Section
- Spirograph
- Spirolateral
- Spline
- Splitting
- Splitting Algorithm
- Sponge
- Sporadic Group
- Sports
- Sprague-Grundy Function
- Sprague-Grundy Number
- Sprague-Grundy Value
- Spread (Link)
- Spread (Tree)
- Spun Knot
- Squarable
- Square
- Square Bracket Polynomial
- Square Cupola
- Square Curve