| 释义 |
Correlation (Statistical)For two variables  and and  , ,
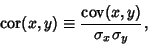 | (1) |
 denotes Standard Deviation and denotes Standard Deviation and  is the Covariance of these two variables. Forthe general case of variables is the Covariance of these two variables. Forthe general case of variables  and and 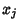 , where , where 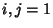 , 2, ..., , 2, ..., 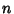 , ,
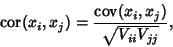 | (2) |
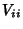 are elements of the Covariance Matrix. In general, a correlation gives the strength of therelationship between variables. The variance of any quantity is alway Nonnegative bydefinition, so are elements of the Covariance Matrix. In general, a correlation gives the strength of therelationship between variables. The variance of any quantity is alway Nonnegative bydefinition, so
 | (3) |
 | (4) |
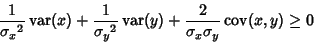 | (5) |
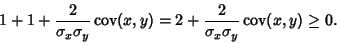 | (6) |
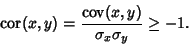 | (7) |
 | (8) |
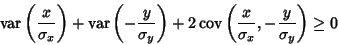 | (9) |
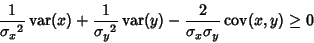 | (10) |
 | (11) |
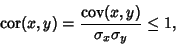 | (12) |
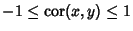 . For a linear combination of two variables, . For a linear combination of two variables,
Examine the cases where  , ,
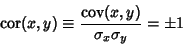 | (14) |
 | (15) |
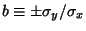 , which requires that the argument of theVariance is a constant. Therefore, , which requires that the argument of theVariance is a constant. Therefore,  , so , so 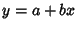 . If . If  , ,  is either perfectlycorrelated ( is either perfectlycorrelated (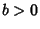 ) or perfectly anticorrelated ( ) or perfectly anticorrelated (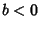 ) with ) with  .See also Covariance, Covariance Matrix, Variance .See also Covariance, Covariance Matrix, Variance |
![]() and
and ![]() ,
,