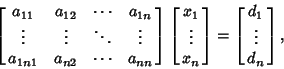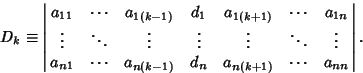| 释义 |
Cramer's RuleGiven a set of linear equations
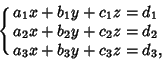 | (1) |
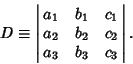 | (2) |
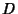 by by  , and use the property of Determinants that Multiplication by aconstant is equivalent to Multiplication of each entry in a given row by that constant , and use the property of Determinants that Multiplication by aconstant is equivalent to Multiplication of each entry in a given row by that constant
 | (3) |
 times column 2 and times column 2 and  times column 3 to column 1, times column 3 to column 1,
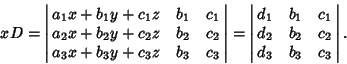 | (4) |
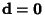 , then (4) reduces to , then (4) reduces to 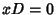 , so the system has nondegenerate solutions (i.e., solutions other than(0, 0, 0)) only if , so the system has nondegenerate solutions (i.e., solutions other than(0, 0, 0)) only if 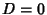 (in which case there is a family of solutions). If (in which case there is a family of solutions). If 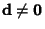 and and 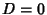 , thesystem has no unique solution. If instead , thesystem has no unique solution. If instead 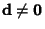 and and  , then solutions are given by , then solutions are given by
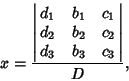 | (5) |
This procedure can be generalized to a set of 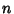 equations so, given a system of equations so, given a system of 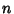 linear equations linear equations
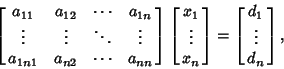 | (8) |
 | (9) |
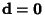 , then nondegenerate solutions exist only if , then nondegenerate solutions exist only if 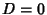 . If . If 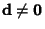 and and 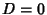 , the system has no unique solution. Otherwise, compute , the system has no unique solution. Otherwise, compute
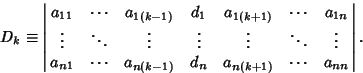 | (10) |
 for for 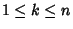 . In the 3-D case, the Vector analog of Cramer's rule is . In the 3-D case, the Vector analog of Cramer's rule is
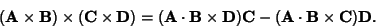 | (11) |
|
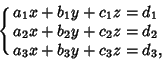
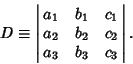

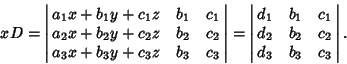
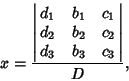

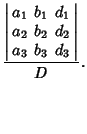
![]() equations so, given a system of
equations so, given a system of ![]() linear equations
linear equations