| 释义 |
Crossing Number (Graph)Given a ``good'' Graph (i.e., one for which all intersecting Edgesintersect in a single point and arise from four distinct Vertices), the crossing number is theminimum possible number of crossings with which the Graph can be drawn. AGraph with crossing number 0 is a Planar Graph. Garey and Johnson (1983) showed thatdetermining the crossing number is an NP-Complete Problem. Guy's Conjecture suggests that the crossing numberfor the Complete Graph  is
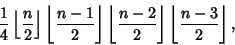 | (1) |
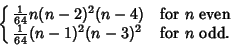 | (2) |
| Order | Predicted | Known | | 1 | 0 | 0 | | 2 | 0 | 0 | | 3 | 0 | 0 | | 4 | 0 | 0 | | 5 | 1 | 1 | | 6 | 3 | 3 | | 7 | 9 | 9 | | 8 | 18 | 18 | | 9 | 36 | 36 | | 10 | 60 | 60 | | 11 | 100 | | | 12 | 150 | | | 13 | 225 | | | 14 | 315 | | | 15 | 441 | | | 16 | 588 | |
Zarankiewicz's Conjecture asserts that the crossing number for a Complete Bigraph is
 | (3) |
 , and Zarankiewicz has shown that, in general, the Formula provides an upperbound to the actual number. The table below gives known results. When the number is not known exactly, the predictionof Zarankiewicz's Conjecture is given in parentheses.| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | 2 | | 0 | 0 | 0 | 0 | 0 | 0 | | 3 | | | 1 | 2 | 4 | 6 | 9 | | 4 | | | | 4 | 8 | 12 | 18 | | 5 | | | | | 16 | 24 | 36 | | 6 | | | | | | 36 | 54 | | 7 | | | | | | | 77, 79, or (81) |
Consider the crossing number for a rectilinear Graph  which may have only straightEdges, denoted 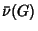 . For a Complete Graph of order  , the rectilinearcrossing number is always larger than the general graph crossing number. The first rectilinear crossing numbers forA014540). The  lower limit is from Singer (1986), who proved that
 | (4) |
 | (5) |
The first few toroidal crossing number for a Complete Graph are 0, 0, 0, 0, 0, 0, 0, 4, 9, 23, 42, 70, 105, 154, 226,326, ... (Sloane's A014543). The toroidal crossing numbers for a Complete Bigraph are given in the following table. | 1 | 0 | 0 | 0 | 0 | 0 | 0 | | 2 | | 0 | 0 | 0 | 0 | 0 | | 3 | | | 0 | 0 | 0 | 0 | | 4 | | | | | 2 | | | 5 | | | | | 5 | 8 | | 6 | | | | | | 12 | | 7 | | | | | | |
ReferencesGardner, M. ``Crossing Numbers.'' Ch. 11 in Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, pp. 133-144, 1986.Garey, M. R. and Johnson, D. S. ``Crossing Number is NP-Complete.'' SIAM J. Alg. Discr. Meth. 4, 312-316, 1983. Guy, R. K. ``Latest Results on Crossing Numbers.'' In Recent Trends in Graph Theory, Proc. New York City Graph Theory Conference, 1st, 1970. (Ed. New York City Graph Theory Conference Staff). New York: Springer-Verlag, 1971. Guy, R. K. and Jenkyns, T. ``The Toroidal Crossing Number of  .'' J. Comb. Th. 6, 235-250, 1969. Guy, R. K.; Jenkyns, T.; and Schaer, J. ``Toroidal Crossing Number of the Complete Graph.'' J. Comb. Th. 4, 376-390, 1968. Jensen, H. F. ``An Upper Bound for the Rectilinear Crossing Number of the Complete Graph.'' J. Comb. Th. Ser. B 10, 212-216, 1971. Kleitman, D. J. ``The Crossing Number of  .'' J. Comb. Th. 9, 315-323, 1970. Singer, D. Unpublished manuscript ``The Rectilinear Crossing Number of Certain Graphs,'' 1971. Quoted in Gardner, M. Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, 1986. Sloane, N. J. A.A014540,A014543, andA000241/M2772in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html. Tutte, W. T. ``Toward a Theory of Crossing Numbers.'' J. Comb. Th. 8, 45-53, 1970. |