| 释义 |
Cross ProductFor Vectors  and and  , ,
 | (1) |
 | (2) |
where  is the angle between is the angle between  and and  , given by the Dot Product , given by the Dot Product
 | (5) |
Identities involving the cross product include
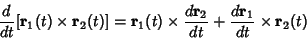 | (6) |
 | (7) |
 | (8) |
 | (9) |
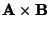 is a Pseudovector, see Arfken (1985, pp. 22-23). In Tensornotation, is a Pseudovector, see Arfken (1985, pp. 22-23). In Tensornotation,
 | (10) |
 is the Levi-Civita Tensor.See also Dot Product, Scalar Triple Product is the Levi-Civita Tensor.See also Dot Product, Scalar Triple Product
References
Arfken, G. ``Vector or Cross Product.'' §1.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 18-26, 1985.
|
![]() and
and ![]() ,
,