“Decimal Expansion”的概念、定义、习题解题方法及翻译-数学辞典

单词

Decimal Expansion

释义

Decimal Expansion

The decimal expansion of a number is its representation in base 10. For example, the decimal expansion of is 625, of is 3.14159..., and of is 0.1111....

If has a finite decimal expansion, then



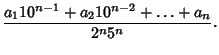			(1)

Factoring possible common multiples gives

(2)

where

(mod 2, 5). Therefore, the numbers with finite decimal expansions are fractions of this form.The number of decimals is given by

. Numbers which have a finite decimal expansion are called Regular Numbers.

Any Nonregular fraction is periodic, and has a period independent of , whichis at most Digits long. If is Relatively Prime to 10, then the period of is adivisor of and has at most Digits, where is the Totient Function. When arational number with is expanded, the period begins after terms and has length , where and are the smallest numbers satisfying

(3)

When

(mod 2, 5),

, and this becomes a purely periodic decimal with

(4)

As an example, consider

. The decimal representation is

. When the Denominator of afraction

has the form

with

, then the period begins after

terms and the length of the period is the exponent to which 10 belongs (mod

), i.e., the number

such that

. If

is Prime and

is Even, then breaking the repeating Digitsinto two equal halves and adding gives all 9s. For example,

, and

. For

with a Prime Denominator other than 2 or 5, all cycles

have the same length (Conway and Guy 1996).

If is a Prime and 10 is a Primitive Root of , then the period of the repeating decimal is given by

(5)

where

is the Totient Function. Furthermore, the decimal expansions for

, with

, 2, ...,

have periods of length

and differ only by a cyclic permutation. Such numbers are called Long Primes by Conway and Guy (1996). An equivalent definition is that

(6)

for

and no

less than this. In other words, a Necessary (but not Sufficient) condition is thatthe number

(where

is a Repunit) is Divisible by

, which means that

is Divisible by

The first few numbers with maximal decimal expansions, called Full Reptend Primes, are 7, 17,19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, ... (Sloane's A001913). The decimals corresponding to these are calledCyclic Numbers. No general method is known for finding Full Reptend Primes. Artin conjectured that Artin's Constant is the fraction of Primes for with has decimal maximal period (Conway and Guy 1996). D. Lehmer has generalized this conjecture to other bases, obtainingvalues which are small rational multiples of .

To find Denominators with short periods, note that

The period of a fraction with Denominator equal to a Prime Factor above is therefore the Powerof 10 in which the factor first appears. For example, 37 appears in the factorization of and , so itsperiod is 3. Multiplication of any Factor by a still gives the same period as the Factoralone. A Denominator obtained by a multiplication of two Factors has a period equal to the firstPower of 10 in which both Factors appear. The following table gives the Primes having smallperiods (Sloane'sA046106,A046107,and A046108; Ogilvy and Anderson 1988).

period	primes
1	3
2	11
3	37
4	101
5	41, 271
6	7, 13
7	239, 4649
8	73, 137
9	333667
10	9091
11	21649, 513239
12	9901
13	53, 79, 265371653
14	909091
15	31, 2906161
16	17, 5882353
17	2071723, 5363222357
18	19, 52579
19	1111111111111111111
20	3541, 27961

A table of the periods of small Primes other than the special , for which the decimal expansion is notperiodic, follows (Sloane's A002371).


3	1	31	15	67	33
7	6	37	3	71	35
11	2	41	5	73	8
13	6	43	21	79	13
17	16	47	46	83	41
19	18	53	13	89	44
23	22	59	58	97	96
29	28	61	60	101	4

Shanks (1873ab) computed the periods for all Primes up to 120,000 and published those up to 29,989.

See also Fraction, Midy's Theorem, Repeating Decimal

References

Conway, J. H. and Guy, R. K. ``Fractions Cycle into Decimals.'' In The Book of Numbers. New York: Springer-Verlag, pp. 157-163 and 166-171, 1996.

Das, R. C. ``On Bose Numbers.'' Amer. Math. Monthly 56, 87-89, 1949.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 159-179, 1952.

Lehmer, D. H. ``A Note on Primitive Roots.'' Scripta Math. 26, 117-119, 1963.

Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, p. 60, 1988.

Rademacher, H. and Toeplitz, O. The Enjoyment of Mathematics: Selections from Mathematics for the Amateur. Princeton, NJ: Princeton University Press, pp. 147-163, 1957.

Rao, K. S. ``A Note on the Recurring Period of the Reciprocal of an Odd Number.'' Amer. Math. Monthly 62, 484-487, 1955.

Shanks, W. ``On the Number of Figures in the Period of the Reciprocal of Every Prime Number Below 20,000.'' Proc. Roy. Soc. London 22, 200, 1873a.

Shanks, W. ``On the Number of Figures in the Period of the Reciprocal of Every Prime Number Between 20,000 and 30,000.'' Proc. Roy. Soc. London 22, 384, 1873b.

Shiller, J. K. ``A Theorem in the Decimal Representation of Rationals.'' Amer. Math. Monthly 66, 797-798, 1959.

Sloane, N. J. A. Sequences A001913/M4353, A002371/M4050, A046106, A046107, and A046108 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''http://www.research.att.com/~njas/sequences/eisonline.html.

随便看

数学辞典收录了8975条数学词条，基本涵盖了常用数学知识及数学英语单词词组的翻译及用法，是数学学习的有利工具。